题目内容
 如图,AB∥EF,AC⊥AB,AB⊥BD,∠E=∠F=120°,则∠DBF+∠CAE等于( )
如图,AB∥EF,AC⊥AB,AB⊥BD,∠E=∠F=120°,则∠DBF+∠CAE等于( )分析:由AB∥EF,∠E=∠F=120°,利用平行线的性质,可求得∠EAB=∠FBA,又由AC⊥AB,AB⊥BD,即可求得∠DBF+∠CAE=∠CAB+∠ABD=90°+90°=180°.
解答:解:∵AB∥EF,∠E=∠F=120°,
∴∠EAB=∠FBA=180°-120°=60°,
∵AC⊥AB,AB⊥BD,
∴∠CAB=∠ABD=90°,
∴∠DBF+∠CAE=∠CAB+∠EAB+∠DBF=∠CAB+∠ABF+∠DBF=∠CAB+∠ABD=90°+90°=180°.
故选C.
∴∠EAB=∠FBA=180°-120°=60°,
∵AC⊥AB,AB⊥BD,
∴∠CAB=∠ABD=90°,
∴∠DBF+∠CAE=∠CAB+∠EAB+∠DBF=∠CAB+∠ABF+∠DBF=∠CAB+∠ABD=90°+90°=180°.
故选C.
点评:此题考查了平行线的性质以及垂线的定义.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
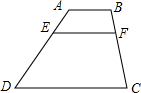 如图,AB∥EF∥CD,AB=2,CD=8,AE:ED=1:5,则EF的长度为
如图,AB∥EF∥CD,AB=2,CD=8,AE:ED=1:5,则EF的长度为 如图,AB∥EF,∠B=46°,∠F=54°,则∠BCF=
如图,AB∥EF,∠B=46°,∠F=54°,则∠BCF= 已知一角的两边与另一个角的两边平行,结合图形,试探索这两个角之间的数量关系.
已知一角的两边与另一个角的两边平行,结合图形,试探索这两个角之间的数量关系. 如图,AB⊥EF,CD⊥EF且AB=CD,则图中全等三角形有
如图,AB⊥EF,CD⊥EF且AB=CD,则图中全等三角形有 已知:如图,AB∥EF,BC⊥CD,则∠α、∠β、∠γ之间的关系是( )
已知:如图,AB∥EF,BC⊥CD,则∠α、∠β、∠γ之间的关系是( )