题目内容
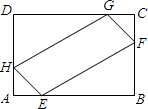 (2013•天桥区二模)在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H,使得AE=AH=CF=CG,如果AB=60,BC=40,四边形EFGH的最大面积是( )
(2013•天桥区二模)在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H,使得AE=AH=CF=CG,如果AB=60,BC=40,四边形EFGH的最大面积是( )分析:设AE=AH=CF=CG=x,四边形EFGH的面积是S.分别求出矩形四个角落的三角形的面积,再利用矩形的面积减去四个角落的三角形的面积,可得四边形EFGH的面积S;先配方,确定函数的对称轴,再与函数的定义域结合即可求出四边形EFGH的面积最大值.
解答:解:设AE=AH=CF=CG=x,四边形EFGH的面积是S.
由题意,BE=DG=60-x,BF=DH=40-x,则
S△AHE=S△CGF=
x2,S△DGH=S△BEF=
(60-x)(40-x),
所以四边形EFGH的面积为:
S=60×40-x2-(60-x)(40-x)=-2x2+(60+40)x=-2(x-25)2+1250(0<x≤40);
当x=25时,S最大值=1250.
故选C.
由题意,BE=DG=60-x,BF=DH=40-x,则
S△AHE=S△CGF=
| 1 |
| 2 |
| 1 |
| 2 |
所以四边形EFGH的面积为:
S=60×40-x2-(60-x)(40-x)=-2x2+(60+40)x=-2(x-25)2+1250(0<x≤40);
当x=25时,S最大值=1250.
故选C.
点评:本题重点考查四边形面积的计算,考查利用配方法求二次函数的最值,应注意函数的对称轴与区间结合,确定分类的标准.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
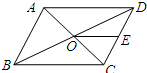 (2013•天桥区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是( )
(2013•天桥区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是( )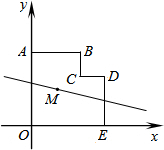 (2013•天桥区二模)如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则下列各点在直线l上的是( )
(2013•天桥区二模)如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则下列各点在直线l上的是( )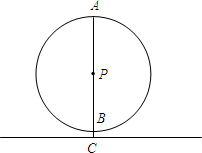 (2013•天桥区二模)如图所示,⊙P表示的是一个摩天轮,最高处A到地面的距离是80.5米,最低处B到地面的距离是0.5米.小红由B处登上摩天轮,乘坐一周需要12分钟.乘坐一周的过程中,小红距离地面的高度是60.5米的时刻是第
(2013•天桥区二模)如图所示,⊙P表示的是一个摩天轮,最高处A到地面的距离是80.5米,最低处B到地面的距离是0.5米.小红由B处登上摩天轮,乘坐一周需要12分钟.乘坐一周的过程中,小红距离地面的高度是60.5米的时刻是第