题目内容
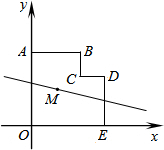 (2013•天桥区二模)如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则下列各点在直线l上的是( )
(2013•天桥区二模)如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则下列各点在直线l上的是( )分析:先延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,由所给点的坐标得出四边形OABC,四边形CDEF都为矩形,并且点M(2,3)是矩形OABF对角线的交点,点N是矩形CDEF的中心,得出直线l必过M和N点,再设直线l的解析式为y=kx+b,利用待定系数法即可求出直线l的函数表达式,然后把所给的点分别代入,即可求出答案.
解答: 解:如图,延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,
解:如图,延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,
∵O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0),
∴四边形OABF为矩形,四边形CDEF为矩形,
∴点M(2,3)是矩形OABF对角线的交点,
∴点M为矩形ABFO的中心,
∴直线l把矩形ABFO分成面积相等的两部分,
同理可证:点N是矩形CDEF的中心,
∴点N(5,2),
∴过点N(5,2)的直线把矩形CDEF分成面积相等的两部分,
∴直线MN就是所求的直线l,
设直线l的解析式为y=kx+b,
把M(2,3)N(5,2)代入上式得:
,
解得:
,
∴所求直线l的函数表达式是:y=-
x+
,
当x=4时,y=
,则A不正确;
当x=5时,y=2,则B正确;
当x=6时,y=
,则C不正确;
当x=0时,y=
,则D不正确;
故选B.
 解:如图,延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,
解:如图,延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,∵O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0),
∴四边形OABF为矩形,四边形CDEF为矩形,
∴点M(2,3)是矩形OABF对角线的交点,
∴点M为矩形ABFO的中心,
∴直线l把矩形ABFO分成面积相等的两部分,
同理可证:点N是矩形CDEF的中心,
∴点N(5,2),
∴过点N(5,2)的直线把矩形CDEF分成面积相等的两部分,
∴直线MN就是所求的直线l,
设直线l的解析式为y=kx+b,
把M(2,3)N(5,2)代入上式得:
|
解得:
|
∴所求直线l的函数表达式是:y=-
| 1 |
| 3 |
| 11 |
| 3 |
当x=4时,y=
| 7 |
| 3 |
当x=5时,y=2,则B正确;
当x=6时,y=
| 5 |
| 3 |
当x=0时,y=
| 11 |
| 3 |
故选B.
点评:本题考查了一次函数的综合,用到的知识点是矩形的性质即过矩形对角线交点的直线平分矩形的面积和待定系数法求解析式,解题的关键是根据图形作出辅助线,求出四边形OABC和四边形CDEF都是矩形.

练习册系列答案
相关题目
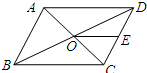 (2013•天桥区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是( )
(2013•天桥区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是( )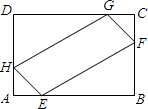 (2013•天桥区二模)在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H,使得AE=AH=CF=CG,如果AB=60,BC=40,四边形EFGH的最大面积是( )
(2013•天桥区二模)在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H,使得AE=AH=CF=CG,如果AB=60,BC=40,四边形EFGH的最大面积是( )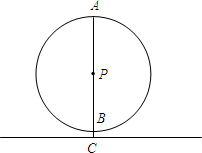 (2013•天桥区二模)如图所示,⊙P表示的是一个摩天轮,最高处A到地面的距离是80.5米,最低处B到地面的距离是0.5米.小红由B处登上摩天轮,乘坐一周需要12分钟.乘坐一周的过程中,小红距离地面的高度是60.5米的时刻是第
(2013•天桥区二模)如图所示,⊙P表示的是一个摩天轮,最高处A到地面的距离是80.5米,最低处B到地面的距离是0.5米.小红由B处登上摩天轮,乘坐一周需要12分钟.乘坐一周的过程中,小红距离地面的高度是60.5米的时刻是第