题目内容
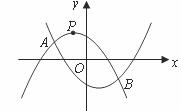
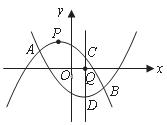
如图,抛物线![]() 相交于
相交于![]() 两点.
两点.
(1)求![]() 值;
值;
(2)设![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),观察
的左边),观察![]() 四点的坐标,写出一条正确的结论,并通过计算说明;
四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设![]() 两点的横坐标分别记为
两点的横坐标分别记为![]() ,若在
,若在![]() 轴上有一动点
轴上有一动点![]() ,且
,且![]() ,过
,过![]() 作一条垂直于
作一条垂直于![]() 轴的直线,与两条抛物线分别交于C,D两点,试问当
轴的直线,与两条抛物线分别交于C,D两点,试问当![]() 为何值时,线段CD有最大值?其最大值为多少?
为何值时,线段CD有最大值?其最大值为多少?
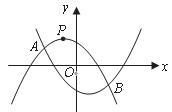
解:(1)![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
解得![]() .
.
(2)由(1)知![]() ,
,![]() 抛物线
抛物线![]() ,
,![]() .
.
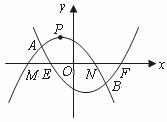
当![]() 时,解得
时,解得![]() ,
,![]() .
.
![]() 点
点![]() 在点
在点![]() 的左边,
的左边,![]() ,
,![]() .
.
当![]() 时,解得
时,解得![]() ,
,![]() .
.
![]() 点
点![]() 在点
在点![]() 的左边,
的左边,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() 点
点![]() 与点
与点![]() 对称,点
对称,点![]() 与点
与点![]() 对称.
对称.
(3)![]() .
.
![]() 抛物线
抛物线![]() 开口向下,抛物线
开口向下,抛物线![]() 开口向上.
开口向上.
根据题意,得![]()
![]() .
.
![]() ,
,![]() 当
当![]() 时,
时,![]() 有最大值
有最大值![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,抛物线y=ax2+bx+c与y轴相交于点C(0,3),与x轴的两个交点分别为A(-1,0)、B(3,0),顶点为D.连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F.
如图,抛物线y=ax2+bx+c与y轴相交于点C(0,3),与x轴的两个交点分别为A(-1,0)、B(3,0),顶点为D.连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F.