题目内容
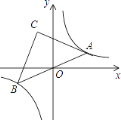
【题目】(2017新疆乌鲁木齐第15题)如图,抛物线![]() 过点
过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,有下列结论:
,有下列结论:
①![]() ;②
;②![]() ;③抛物线经过点
;③抛物线经过点![]() 与点
与点![]() ,则
,则![]() ;④无论
;④无论![]() 取何值,抛物线都经过同一个点
取何值,抛物线都经过同一个点![]() ;⑤
;⑤![]() ,其中所有正确的结论是__________.
,其中所有正确的结论是__________.
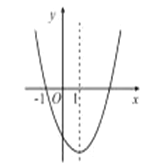
【答案】②④⑤.
【解析】
由图象可知,抛物线开口向上,则a>0,
顶点在y轴右侧,则b<0,
抛物线与y轴交于负半轴,则c<0,
∴abc>0,故①错误;
∵抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,
∴抛物线y=ax2+bx+c过点(3,0),
∴当x=3时,y=9a+3b+c=0,
∵a>0,
∴10a+3b+c>0,故②正确;
∵对称轴为x=1,且开口向上,
∴离对称轴水平距离越大,函数值越大,
∴y1<y2,故③错误;
当x=﹣![]() 时,y=a(﹣
时,y=a(﹣![]() )2+b(﹣
)2+b(﹣![]() )+c=
)+c=![]() ,
,
∵当x=﹣1时,y=a﹣b+c=0,
∴当x=﹣![]() 时,y=a(﹣
时,y=a(﹣![]() )2+b(﹣
)2+b(﹣![]() )+c=0,
)+c=0,
即无论a,b,c取何值,抛物线都经过同一个点(﹣![]() ,0),故④正确;
,0),故④正确;
x=m对应的函数值为y=am2+bm+c,
x=1对应的函数值为y=a+b+c,
又∵x=1时函数取得最小值,
∴am2+bm+c≥a+b+c,即am2+bm≥a+b,
∵b=﹣2a,
∴am2+bm+a≥0,故⑤正确;
故答案为②④⑤.

 名校课堂系列答案
名校课堂系列答案【题目】如图,在半![]() 中,P是直径AB上一动点,且
中,P是直径AB上一动点,且![]() ,过点P作
,过点P作![]() 交半
交半![]() 于点C,P为垂足,连接BC,过点P作
于点C,P为垂足,连接BC,过点P作![]() 于点D.
于点D.
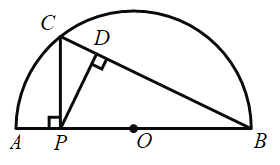
小明根据学习函数的经验,对线段AP,CP,PD的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于动点P在AB上的不同位置,画图,测量,得到了线段AP,CP,PD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | 位置10 | |
| 0.37 | 0.88 | 1.59 | 2.01 | 2.44 | 3.00 | 3.58 | 4.37 | 5.03 | 5.51 |
| 1.45 | 2.12 | 2.65 | 2.83 | 2.95 | 3.00 | 2.95 | 2.67 | 2.21 | 1.65 |
| 1.40 | 1.96 | 2.27 | 2.31 | 2.27 | 2.13 | 1.87 | 1.39 | 0.89 | 0.48 |
在AP,CP,PD的长度这三个量中,确定________的长度是自变量, ________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当![]() 时,AP的长度约为________.
时,AP的长度约为________.