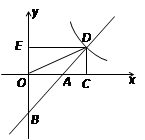题目内容
如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与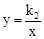 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
(1)求一次函数与反比例函数的解析式;
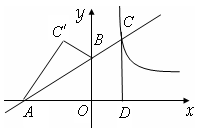
(2)若点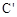 是点C关于y轴的对称点,请求出△
是点C关于y轴的对称点,请求出△ 的面积。
的面积。
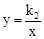 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
(1)求一次函数与反比例函数的解析式;
(2)若点
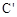 是点C关于y轴的对称点,请求出△
是点C关于y轴的对称点,请求出△ 的面积。
的面积。解:(1)∵直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),
∴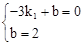 ,解得
,解得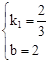 。
。
∴一次函数的解析式为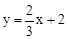 。
。
∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4。
∴C(3,4)。
∵点C在双曲线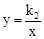 上,∴
上,∴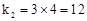 。
。
∴反比例函数的解析式为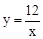 。
。
(2)∵点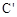 是点C(3,4)关于y轴的对称点,∴
是点C(3,4)关于y轴的对称点,∴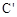 (-3,4)。
(-3,4)。
∴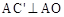 。∴△
。∴△ 的面积等于梯形
的面积等于梯形 减△
减△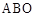 。
。
∴ 。
。
∴
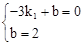 ,解得
,解得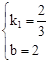 。
。∴一次函数的解析式为
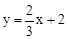 。
。∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4。
∴C(3,4)。
∵点C在双曲线
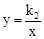 上,∴
上,∴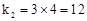 。
。∴反比例函数的解析式为
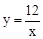 。
。(2)∵点
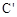 是点C(3,4)关于y轴的对称点,∴
是点C(3,4)关于y轴的对称点,∴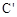 (-3,4)。
(-3,4)。∴
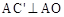 。∴△
。∴△ 的面积等于梯形
的面积等于梯形 减△
减△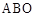 。
。∴
 。
。试题分析:(1)由直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),用待定系数法即可求得一次函数的解析式;由OB是△ACD的中位线可得点C坐标,代入
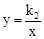 ,即可求得反比例函数的解析式。
,即可求得反比例函数的解析式。(2)由点
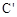 是点C(3,4)关于y轴的对称点,根据关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数,得
是点C(3,4)关于y轴的对称点,根据关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数,得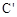 (-3,4),知
(-3,4),知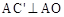 ,从而由
,从而由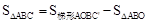 求解。
求解。
练习册系列答案
相关题目
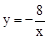 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.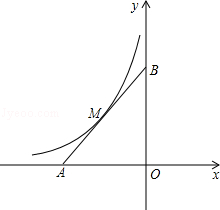
 交于点B(2,1).
交于点B(2,1).
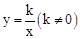 的图象在同一直角坐标系下的大致图象如图所示,则k、b的取值范围是
的图象在同一直角坐标系下的大致图象如图所示,则k、b的取值范围是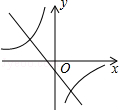
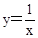 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),则点P3的坐标是 ;点Pn的坐标是 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),则点P3的坐标是 ;点Pn的坐标是 (用含n的式子表示).
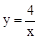 的图象在第一象限内交于点B,点C是函数
的图象在第一象限内交于点B,点C是函数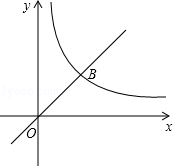
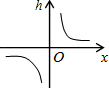
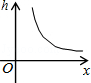
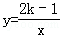 ,当x<0时,y随x的增大而减小,则k的范围( )
,当x<0时,y随x的增大而减小,则k的范围( )
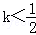

 于点D,过D作两坐标轴的垂线DC、DE,连接OD.
于点D,过D作两坐标轴的垂线DC、DE,连接OD.