题目内容
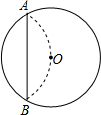如图，⊙O的半径R=3．将弧AB沿弦AB对折，恰好弧AB过圆心O．则弦AB的长为
- A.5
- B.4
- C.
- D.
D
分析：过O点作OD⊥AB，垂足为D，交⊙O于C点，连OA，AC，得到AD=BD，弧AC=弧BC，而弧AB沿弦AB对折，恰好弧AB过圆心O，所以△ACO为等边三角形，并且AD为等边三角形的高，而它的边长为3，由此得到AD，得到AB．
解答：
解：过O点作OD⊥AB，垂足为D，交⊙O于C点，连OA，AC，如图，
则AD=BD，弧AC=弧BC，
∵弧AB沿弦AB对折，恰好弧AB过圆心O，
∴△ACO为等边三角形，并且AD为等边三角形的高，
而OA=3，
∴AD=
OA=
，
所以AB=3．
故选D．
点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理和等边三角形的性质．
分析：过O点作OD⊥AB，垂足为D，交⊙O于C点，连OA，AC，得到AD=BD，弧AC=弧BC，而弧AB沿弦AB对折，恰好弧AB过圆心O，所以△ACO为等边三角形，并且AD为等边三角形的高，而它的边长为3，由此得到AD，得到AB．
解答：
解：过O点作OD⊥AB，垂足为D，交⊙O于C点，连OA，AC，如图，则AD=BD，弧AC=弧BC，
∵弧AB沿弦AB对折，恰好弧AB过圆心O，
∴△ACO为等边三角形，并且AD为等边三角形的高，
而OA=3，
∴AD=
OA=，所以AB=3
．故选D．
点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理和等边三角形的性质．
练习册系列答案
相关题目
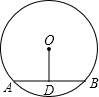如图，⊙O的半径为5cm，圆心O到弦AB的距离OD为3cm，则弦AB的长为
21、如图，⊙O的半径OD经过弦AB（不是直径）的中点C，过AB的延长线上一点P作⊙O的切线PE，E为切点，PE∥OD；延长直径AG交PE于点H；直线DG交OE于点F，交PE于点K．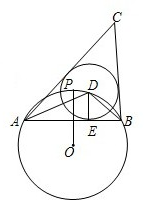
如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP．点D是弦AB所对劣弧上的任一点（异于点A、B），过点D作DE⊥AB于点E，以点D为圆心，DE长为半径作⊙D，连接AD、BD．分别过点A、B作⊙D的切线，两条切线交于点C．下列结论：
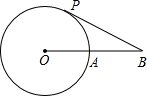如图，⊙O的半径为3cm，B为⊙O外一点，OB交⊙O于点A，AB=OA，动点P从点A出发，以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止．当点P运动的时间为（ ）s时，BP与⊙O相切．
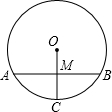如图，⊙O的半径为5cm，若AB是⊙O的一条弦，AB的弦心距OM为3cm，则弦AB的长是