题目内容
【题目】如图,平行四边形ABCD中,AB=2,∠A=60°,以AB为直径的⊙O过点D,点M是BC边上一点(点M不与B,C重合),过点M作BC的垂线MN,交CD边于点N.

(1)求AD的长;
(2)当点N在⊙O上时,求证:直线MN是⊙O的切线;
(3)以CN为直径作⊙P,设BM=x,⊙P的直径为y,
①求y关于x的函数关系式,并写出x的取值范围;
②当BM为何值时,⊙P与⊙O相切.
【答案】(1)1;(2)见解析;(3)①y=2﹣2x(0<x<1);②BM为1时,⊙P与⊙O相切.
【解析】
试题分析:(1)连接OD,由题意证出△AOD是等边三角形,得出AD=OA=1即可;
(2)连接ON,由平行四边形的性质得出AB∥CD,BC=AD=1,∠C=∠A=60°,证出△DON是等边三角形,得出∠DNO=60°,求出∠CNM=30°,因此∠ONM=90°即可;
(3)①由含30°角的直角三角形的性质得出CN=2CM,即可得出结果;
②作PE⊥AB于E,CN⊥AB于N,则∠BCN=30°,由含30°角的直角三角形的性质得出BN=![]() BC=
BC=![]() ,得出PE=CN=
,得出PE=CN=![]() ,由相切两圆的圆心距=两圆半径之和,得出OP=OB+PC=2﹣x,因此OE=OB+BN﹣EN=
,由相切两圆的圆心距=两圆半径之和,得出OP=OB+PC=2﹣x,因此OE=OB+BN﹣EN=![]() +x,由勾股定理得出方程,解方程即可.
+x,由勾股定理得出方程,解方程即可.
(1)解:连接OD,如图1所示:
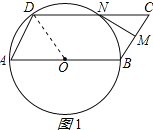
根据题意得:OA=OB=1,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴AD=OA=1,∠AOD=60°;
(2)证明:连接ON,如图2所示:

∵四边形ABCD是平行四边形,
∴AB∥CD,BC=AD=1,∠C=∠A=60°,
∴∠ODN=∠AOD=60°,
∵OD=ON,
∴△DON是等边三角形,
∴∠DNO=60°,
∵MN⊥BC,
∴∠CNM=90°﹣60°=30°,
∴∠ONM=180°﹣30°﹣60°=90°,
即MN⊥ON,
∴直线MN是⊙O的切线;
(3)解:①∵∠CNM=30°,MN⊥BC,
∴CN=2CM,即y=2(1﹣x),
∴y=2﹣2x,
即y关于x的函数关系式为y=2﹣2x(0<x<1);
②作PE⊥AB于E,CN⊥AB于N,如图3所示:
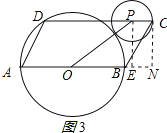
则∠BCN=30°,
∴BN=![]() BC=
BC=![]() ,PE=CN=
,PE=CN=![]() ,
,
∵⊙P与⊙O相切,
∴OP=OB+PC=1+1﹣x=2﹣x,OE=OB+BN﹣EN=1+![]() ﹣(1﹣x)=
﹣(1﹣x)=![]() +x,
+x,
由勾股定理得:OE2+PE2=OP2,
即(![]() +x)2+(
+x)2+(![]() )2=(2﹣x)2,
)2=(2﹣x)2,
解得:x=1,
即BM为1时,⊙P与⊙O相切.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案