题目内容
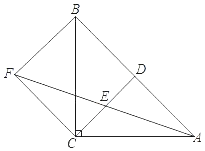
【题目】如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF
⑴求证:四边形ABCD是平行四边形.
⑵若∠BAE=∠BDC,AE=3,BD=9,AB=4,求四边形ABCD的周长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由垂直得到∠EAD=∠FCB=90°,根据AAS可证明Rt△AED≌Rt△CFB,得到AD=BC,根据平行四边形的判定判断即可;
(2)由平行四边形ABCD的性质可得:AB//CD,从而得到∠ABE=∠BDC,又由∠BAE=∠BDC可得:∠ABE=∠BAE,从而得出BE=AE=3,DE=BD-BE=6,在Rt△AED中,根据勾股定理求得AD的长度,再求其周长即可.
(1)∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°,
∵AD∥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
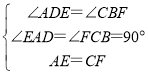 ,
,
∴Rt△AED≌Rt△CFB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB//CD,
∴∠ABE=∠BDC,
又∵∠BAE=∠BDC,
∴∠ABE=∠BAE,
∴BE=AE=3,
∴DE=BD-BE=6,
在Rt△AED中,AD=![]() ,
,
∴四边形ABCD的周长为2(![]() +4)=
+4)=![]() .
.

练习册系列答案
相关题目