题目内容
王英同学从A地沿北偏西60°方向走100米到B地，再从B地向正南方向走200米到C地，此时王英同学离A地的距离是分析：先在直角△ABE中利用三角函数求出BE和AE，然后在直角△ACF中，利用勾股定理求出AC．
解答：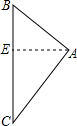
解：如图，作AE⊥BC于点E．
∵∠EAB=30°，AB=100，
∴BE=50，AE=50
．
∵BC=200，
∴CE=150．
在Rt△ACE中，根据勾股定理得：AC=100
．
即此时王英同学离A地的距离是100
米．
故答案为：100
．
解：如图，作AE⊥BC于点E．∵∠EAB=30°，AB=100，
∴BE=50，AE=50
| 3 |
∵BC=200，
∴CE=150．
在Rt△ACE中，根据勾股定理得：AC=100
| 3 |
即此时王英同学离A地的距离是100
| 3 |
故答案为：100
| 3 |
点评：解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
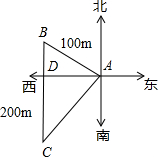王英同学从A地沿北偏西60°方向走100m到B地，再从B地向正南方向走200m到C地，此时王英同学离A地（ ）A、50
| ||
| B、100m | ||
| C、150m | ||
D、100
|
王英同学从A地沿北偏西60º方向走100m到B地，再从B地向正南方向走200m到C地，此时王英同学离A地（ ）.
A． m | B．100m | C．150m | D． m |
m B．100m C．150m D．
m