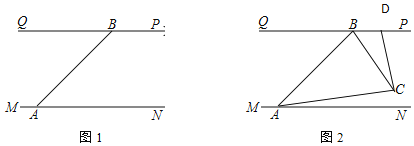题目内容
【题目】如图，已知直线
交x轴于A，交y轴于B，过B作
，且
，点C在第四象限，点
．
求点A，B，C的坐标；
点M是直线AB上一动点，当
最小时，求点M的坐标；
点P、Q分别在直线AB和BC上，
是以RQ为斜边的等腰直角三角形
直接写出点P的坐标．
【答案】(1)A(-3,0),B(0,2),C(2,-1);(2)
;(3) P的坐标为
或
【解析】
（1）根据一次函数解析式先求出A、B坐标，再证明
≌
，即可求解；
（2）作点C关于直线AB的对称点C′，连结R C′交直线AB于M，确定直线R C′的解析式即可求解；
（3）分点P在第一、二象限两种情况，分别求解即可．
解：
当
时，
，
当
时，
，
，
过C作
轴，垂足为H，
，
，
，
，
≌
，
，
，
，
，
作点C关于直线AB的对称点C′，
点C′在直线BC上，且C′（-2,5）
连结 RC′交直线AB于M，
设直线RC′的解析式为
则
，解得
，
，
，
；
当点P在第二象限时，如下图，
过点P作y轴的平行线交过点Q与x轴的平行线于点G，交x轴于点H，延长GQ交y轴于点M，
，
，
，
又
，
，
≌
，
，
，
设：点P、Q的坐标分别为
、
，
，即：
，，即：
，
联立
并解得：
，
故点P的坐标，
当点P在第一象限时，
同理可得：点P的坐标为
，
故：点P的坐标为或
练习册系列答案
相关题目
