题目内容
阅读下面的问题,并解答题(1)和题(2)。
如图①所示,P是等腰△ABC的底边BC上任一点,PE⊥AB于E,PF⊥AC于F,BH是腰AC上的高,求证:PE+PF=BH。

![]() ,
,
![]()
因为AB=AC,所以BH=PE+PF
按照上述证法或用其它方法证明下面两题:
(1)如图②,P是边长为2的正方形ABCD边CD上任意一点,且PE⊥DB于E,PF⊥CA于F,求PE+PF的值。
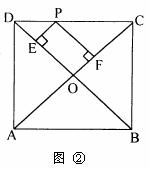
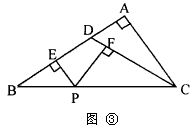
(2)如图③,在△ABC中,∠A=90°,D是AB上一点,且BD=CD,过BC
![]()
求PE+PF的值
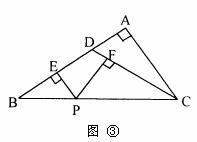
解:(1)在△BOC中,∠COB=90°,BC=2,CO=BO
![]()
![]()
(2)如图,连结PD,由面积关系得:
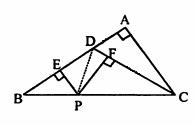
![]()
由题意知,![]()
![]()
![]()
下面求AC的值:
设AD=x,则BD=CD=3x,![]()
![]()
![]() , 解得:x=2(负值舍去)
, 解得:x=2(负值舍去)
![]()

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
| 阅读下面的问题,并解答题(1)和题(2)。 | ||
(1)如图②,P是边长为2的正方形ABCD边CD上任意一点,且PE⊥DB于E,PF⊥CA于F,求PE+PF的值。 | ||
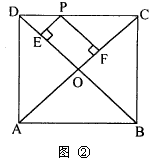 | ||
(2)如图③,在△ABC中,∠A=90°,D是AB上一点,且BD=CD,过BC上任一点P做PE⊥AB于E,PF⊥DC于F,已知AD:BD=1:3,BC= 4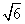 ,求PE+PF的值。 ,求PE+PF的值。 | ||
 |
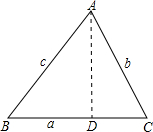 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.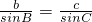
 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明. ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.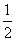 AC×BH=
AC×BH=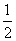 AC×PF+
AC×PF+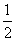 AB×PE
AB×PE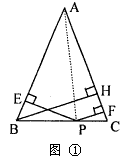

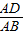 ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC
 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.