题目内容
阅读下面的材料,并回答所提出的问题:如图所示,在锐角三角形ABC中,求证: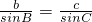
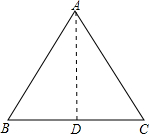
这个三角形不是一个直角三角形,不能直接使用锐角三角函数的知识去处理,所以必须构造直角三角形, 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
解:如图,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,sinB= ,则AD=csinB
,则AD=csinB
Rt△ACD中,sinC= ,则AD=bsinC
,则AD=bsinC
所以c sinB=b sinC,即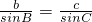
(1)在上述分析证明过程中,主要用到了下列三种数学思想方法的哪一种
A、数形结合的思想;B、转化的思想;C、分类的思想
(2)用上述思想方法解答下面问题.
在△ABC中,∠C=60°,AC=6,BC=8,求AB和△ABC的面积.
(3)用上述结论解答下面的问题(不必添加辅助线)
在锐角三角形ABC中,AC=10,AB= ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.
解:(1)由分析知选B;
(2)过A作AD⊥C于D,在直角三角形ACD中,AC=6,∠C=60°,
 AD=AC•sin60°=3
AD=AC•sin60°=3 ,CD=AC•cos60°=3,
,CD=AC•cos60°=3,
∴BD=BC-CD=8-3=5,
直角三角形ABD中,根据勾股定理可得,
AB= =
= ,
,
S= •BC•DA=
•BC•DA=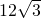 ,
,
(3)由题意可得: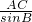 =
=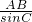 ,
,
即: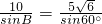 ,
,
∴sinB= ,
,
因此∠B=45°.
分析:(1)题中给出的解题的过程是通过构建直角三角形,以AD为中间值将相等的条件进行转化而得出的结果,因此应该选B;
(2)根据题目给出的解题方法,我们也要通过构建直角三角形来求解,过A作AD⊥BC于D,那么先求两直角三角形的公共边AD是解题的关键,可在三角形ACD中求出AD,CD的长,然后在三角形ABD中求出AB的长,有了AD,BC的长也就能求出三角形的面积了;
(3)可将AC,AB,sinC的值代入题目给出的等量条件中求出sinB的值,也就求出了∠B的度数.
点评:本题就是一个先学习再运用过程,目的考查学生综合能力,首先看懂,然后理解再应用,本题的重点是要学会题中给出的作辅助线的方法.
(2)过A作AD⊥C于D,在直角三角形ACD中,AC=6,∠C=60°,
 AD=AC•sin60°=3
AD=AC•sin60°=3 ,CD=AC•cos60°=3,
,CD=AC•cos60°=3,∴BD=BC-CD=8-3=5,
直角三角形ABD中,根据勾股定理可得,
AB=
 =
= ,
,S=
 •BC•DA=
•BC•DA=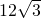 ,
,(3)由题意可得:
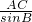 =
=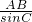 ,
,即:
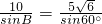 ,
,∴sinB=
 ,
,因此∠B=45°.
分析:(1)题中给出的解题的过程是通过构建直角三角形,以AD为中间值将相等的条件进行转化而得出的结果,因此应该选B;
(2)根据题目给出的解题方法,我们也要通过构建直角三角形来求解,过A作AD⊥BC于D,那么先求两直角三角形的公共边AD是解题的关键,可在三角形ACD中求出AD,CD的长,然后在三角形ABD中求出AB的长,有了AD,BC的长也就能求出三角形的面积了;
(3)可将AC,AB,sinC的值代入题目给出的等量条件中求出sinB的值,也就求出了∠B的度数.
点评:本题就是一个先学习再运用过程,目的考查学生综合能力,首先看懂,然后理解再应用,本题的重点是要学会题中给出的作辅助线的方法.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目