题目内容
【题目】已知直线l1:y=﹣![]() 与直线l2:y=kx﹣
与直线l2:y=kx﹣![]() 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
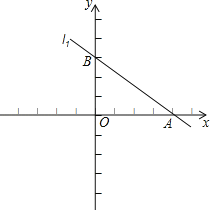
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由.
【答案】(1)k=![]() ,见解析;(2)点P的坐标(
,见解析;(2)点P的坐标(![]() ,
,![]() );(3)当N的纵坐标为(
);(3)当N的纵坐标为(![]() ,﹣
,﹣![]() )时,△ANM≌△AOC.
)时,△ANM≌△AOC.
【解析】
试题分析:(1)对于直线l1,令y=0求出x的值,确定出A坐标,代入直线l2求出k的值,作出直线l2图象即可;
(2)设P(a,b),△ACP面积=△ABC面积﹣△BPC面积,根据已知三角形ACP面积求出a的值,进而求出b的值,确定出P坐标即可;
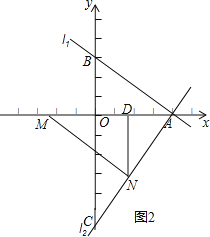
(3)如图2,作ND⊥x轴于D,利用勾股定理求出AC的长,由△ANM≌△AOC,得到对应边相等,表示出AM,AN,MN,确定出△AMN为直角三角形,利用面积法求出ND的长,确定出N纵坐标,进而求出横坐标,确定出N坐标即可.
解:(1)∵直线l1:y=﹣![]() x+3与x轴交于点A,
x+3与x轴交于点A,
∴令y=0时,x=4,即A(4,0),
将A(4,0)代入直线l2:y=kx﹣![]() ,得k=
,得k=![]() ,
,
直线l2图象如图1所示;
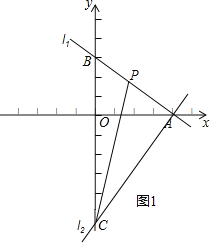
(2)设P(a,b),
根据题意得:S△ACP=S△ABC﹣S△PBC=![]() ×(3+
×(3+![]() )×4﹣
)×4﹣![]() ×(3+
×(3+![]() )a=15,
)a=15,
解得:a=![]() ,
,
将P(![]() ,b)代入直线l1得:b=
,b)代入直线l1得:b=![]() ×(﹣
×(﹣![]() )+3=﹣
)+3=﹣![]() +3=
+3=![]() ,
,
∴点P的坐标(![]() ,
,![]() );
);
(3)如图2,作ND⊥x轴于D,
∵AC=![]() =
=![]() ,△ANM≌△AOC,
,△ANM≌△AOC,
∴AM=AC=![]() ,AN=AO=4,MN=OC=
,AN=AO=4,MN=OC=![]() ,∠ANM=∠AOC=90°,
,∠ANM=∠AOC=90°,
∵S△AMN=![]() AMND=
AMND=![]() ANMN,
ANMN,
∴ND=![]() =
=![]() =
=![]() ,
,
将N的纵坐标y=﹣![]() 代入直线l2得:x=
代入直线l2得:x=![]() ,
,
∴当N的纵坐标为(![]() ,﹣
,﹣![]() )时,△ANM≌△AOC.
)时,△ANM≌△AOC.