题目内容
【题目】如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A出发沿AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿BC以2cm/s的速度向点C移动，几秒种后△DPQ的面积为31cm2？
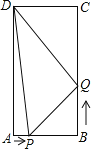
【答案】运动1秒或5秒后△DPQ的面积为31cm2．
【解析】
设运动x秒钟后△DPQ的面积为31cm2，则AP=xcm，BP=（6-x）cm，BQ=2xcm，CQ=（12-2x）cm，利用分割图形求面积法结合△DPQ的面积为31cm2，即可得出关于x的一元二次方程，解之即可得出结论
解：设运动x秒钟后△DPQ的面积为31cm2，则AP=xcm，BP=（6-x）cm，BQ=2xcm，CQ=（12-2x）cm，
S△DPQ=S矩形ABCD-S△ADP-S△CDQ-S△BPQ，
=ABBC-
ADAP-CDCQ-BPBQ，
=6×12-×12x-×6（12-2x）-（6-x）2x，
=x2-6x+36=31，
解得：x1=1，x2=5．
答：运动1秒或5秒后△DPQ的面积为31cm2．
练习册系列答案
相关题目
