题目内容
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
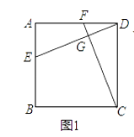
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;
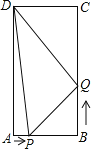
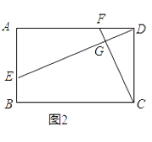
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由四边形ABCD为正方形,利用正方形的性质得到一对角为直角,相等,且AD=DC,利用同角的余角相等得到一对角相等,利用AAS得到三角形ADE与三角形DCF全等,利用全等三角形对应边相等即可得证;
(2)由四边形ABCD为矩形,得到一对直角相等,利用同角的余角相等得到一对角相等,利用两对角相等的三角形相似得到三角形ADE与三角形DCF相似,利用相似三角形对应边成比例即可得证.
(1)∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,
∴∠AED=∠CFD,
∴△ADE≌△DCF,
∴DE=CF
(2)∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,∠DCF+∠CFD=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴![]()

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目