题目内容
【题目】如图，是一个圆柱形的饼干盒，在盒子外侧下底面的点A处有甲、乙两只蚂蚁，它们都想要吃到上底面外侧B′处的食物：甲蚂蚁沿A→A′→B′的折线爬行，乙蚂蚁沿圆柱的侧面爬行：若∠AOB=∠A′O′B′=90°（AA′、BB′都与圆柱的中轴线OO′平行），圆柱的底面半径是12cm，高为1cm，则：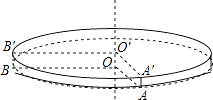 
（1）A′B′=cm，甲蚂蚁要吃到食物需爬行的路程长l1=cm；
（2）乙蚂蚁要吃到食物需爬行的最短路程长l2=cm（π取3）；
（3）若两只蚂蚁同时出发，且爬行速度相同，在乙蚂蚁采取最佳策略的前提下，哪只蚂蚁先到达食物处？请你通过计算或合理的估算说明理由．（参考数据：π取3， 
≈1.4）
【答案】
（1）12 
；12 +1
（2）5 
（3）解：∵l1=12 +1≈12×1.2+1=15.4
∴ 
=237.16．
∵ 
= 
=324，
∴ 
．
∴l1＜l2．
∴甲蚂蚁先到达食物处
【解析】解：（1）∵∠A′O′B′=90°，O′A′=O′B′，
∴A′B′=A′B′= A′O′=12 ．
∴l1=A′B′+AA′=12 +1．
故答案为：12 ；12 +1．
2） 
= 
=6π=18．
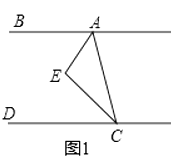
将圆柱体的侧面展开得到如图1所示矩形AA′B′B．
∵ =18，
∴A′B′=18．
在Rt△ABB′中，AB′= 
= 
=5 ．
故答案为：5 ．
（1）由∠A′O′B′=90°，可知△B′A′O′为等腰直角三角形，故此A′B′= A′O′，然后根据l1=A′B′+AA′求解即可；（2）先求得弧A′B′的长，然后根据勾股定理求得矩形AA′B′B的对角线的长度即可；（3）将 ≈1.4代入从而可求得l1、l2的近似值，从而可作出判断．
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
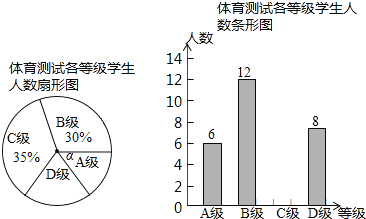
【题目】我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀，这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表（不完整）如下所示：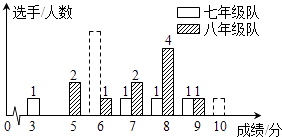 
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | m | 3.41 | 90% | 20% | |
八年级 | 7.1 | n | 80% | 10% |
（1）观察条形统计图，可以发现：八年级成绩的标准差 ， 七年级成绩的标准差（填“＞”、“＜”或“=”），表格中m= ， n=；
（2）计算七年级的平均分；
（3）有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．
