题目内容
【题目】已知: ![]() =8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
=8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
【答案】解:∵ ![]() =8, ∴a=11或﹣5,
=8, ∴a=11或﹣5,
∴点A(1,11)或(1,﹣5),
∴关于y轴的对称点为点B为(﹣1,11)或(﹣1,﹣5),
∵将点B向下平移2个单位后,再向左平移3个单位得到点C,
∴C(﹣1﹣3,11﹣2)或(﹣1﹣3,﹣5﹣2),
即:C(﹣4,9)或(﹣4,﹣7),
①当C(﹣4,9)时,与原点及x轴所围成的三角形的面积为:
S△ACO=5×11﹣ ![]() ×2×5﹣
×2×5﹣ ![]() ×4×9﹣
×4×9﹣ ![]() ×1×11=26.5;
×1×11=26.5;
①当C′(﹣4,﹣7)时,与原点及x轴所围成的三角形的面积为:
S△C′OA′=5×7﹣ ![]() ×1×5﹣
×1×5﹣ ![]() ×5×2﹣
×5×2﹣ ![]() ×4×7=13.5.
×4×7=13.5.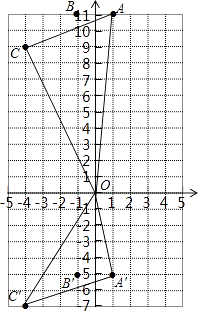
【解析】利用算术平方根的定义以及三角形面积求法和图形的平移,得出对应点坐标进而求出即可.
【考点精析】根据题目的已知条件,利用算数平方根和坐标与图形变化-平移的相关知识可以得到问题的答案,需要掌握正数a的正的平方根叫做a的算术平方根;正数和零的算术平方根都只有一个,零的算术平方根是零;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.

练习册系列答案
相关题目