题目内容
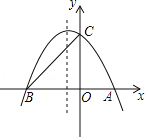
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点B的坐标为(﹣3,0),点C的坐标为(0,3),
(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点H,使CH+AH的值最小,求出点H的坐标;
(3)在抛物线上存在点P,满足S△AOP=5,
请求出点P的坐标;
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)(﹣
x+3;(2)(﹣![]() ,
,![]() );(3)P点坐标为(
);(3)P点坐标为(![]() ,﹣5)或(
,﹣5)或(![]() ,﹣5);
,﹣5);
【解析】
(1)设交点式y=a(x-2)(x+3),然后把C点坐标代入求出a即可;
(2)如图1,先利用待定系数法求出直线BC的解析式为y=x+3,再确定抛物线的对称轴方程,设直线BC与直线x=-![]() 相交于点H,根据抛物线的对称性得HB=HA,根据两点之间线段最短可判定此时HA+HC的值最小,从而得到此时点H的坐标;
相交于点H,根据抛物线的对称性得HB=HA,根据两点之间线段最短可判定此时HA+HC的值最小,从而得到此时点H的坐标;
(3)如图1,设P(x,-![]() x2-
x2-![]() x+3),利用三角形面积公式得∴2|-
x+3),利用三角形面积公式得∴2|-![]() x2-
x2-![]() x+3|=5,然后解两个一元二次方程可求出满足条件的P点坐标;
x+3|=5,然后解两个一元二次方程可求出满足条件的P点坐标;
(1)设抛物线的解析式为y=a(x﹣2)(x+3),
把C(0,3)代入得a(﹣2)3=3,解得a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x﹣2)(x+3),
(x﹣2)(x+3),
即y=﹣![]() x2-
x2-![]() x+3;
x+3;
(2)如图1,设直线BC的解析式为y=kx+b,
把B(﹣3,0),C(0,3)代入得![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=x+3,
抛物线的对称轴为直线x=﹣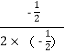 =﹣
=﹣![]() ,
,
直线BC与直线x=﹣![]() 相交于点H,则HB=HA,
相交于点H,则HB=HA,
∵HA+HC=HB+HC=BC,
∴此时HA+HC的值最小,点H的坐标为(﹣![]() ,
,![]() );
);
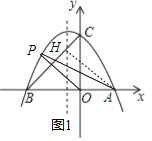
(3)如图1,设P(x,﹣![]() x2﹣
x2﹣![]() x+3),
x+3),
∵S△AOP=5,
∴![]() 2|﹣
2|﹣![]() x2﹣
x2﹣![]() x+3|=5,
x+3|=5,
∴﹣![]() x2﹣
x2﹣![]() x+3=5或﹣
x+3=5或﹣![]() x2﹣
x2﹣![]() x+3=﹣5,
x+3=﹣5,
方程﹣![]() x2﹣
x2﹣![]() x+3=5没有实数解;
x+3=5没有实数解;
解方程﹣![]() x2﹣
x2﹣![]() x+3=﹣5得x1=
x+3=﹣5得x1=![]() ,x2=
,x2=![]() ,
,
∴P点坐标为(![]() ,﹣5)或(
,﹣5)或(![]() ,﹣5);
,﹣5);

 阅读快车系列答案
阅读快车系列答案【题目】某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
销售额(万元) | 17 | 19 | 20 | 21 | 25 | 26 | 28 | 30 |
频数(人数) | 1 | 1 | 3 | 3 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.