Question

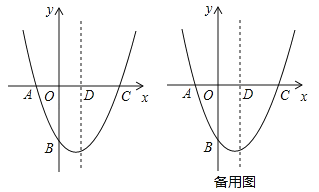
【题目】如图，在平面直角坐标系中，二次函数的图象经过点A（﹣1，0），B（0，），C（2，0），其对称轴与x轴交于点D．

（1）求二次函数的表达式及其顶点坐标；

（2）若P为y轴上的一个动点，连接PD，则PB+PD的最小值为 ；

（3）M（x，t）为抛物线对称轴上一动点．

①若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，则这样的点N共有 个；

②连接MA，MB，若∠AMB不小于60°，求t的取值范围．

Answer 1

【答案】（1），顶点坐标（，）；（2）；（3）①5；②≤t≤．

【解析】（1）由题意得：，解得：，∴抛物线解析式为，∵=，∴顶点坐标（，）．

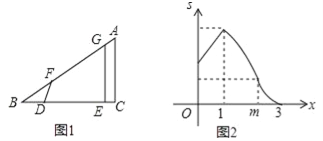
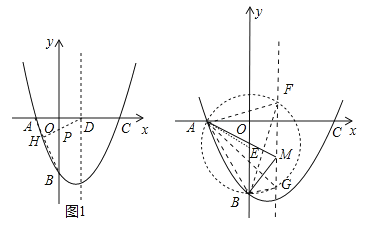
（2）如图1中，连接AB，作DH⊥AB于H，交OB于P，此时PB+PD最小．

理由：∵OA=1，OB=，∴tan∠ABO=，∴∠ABO=30°，∴PH=PB，∴PB+OD=PH+PD=DH，∴此时PB+PD最短（垂线段最短）．

在RT△ADH中，∵∠AHD=90°，AD=，∠HAD=60°，∴sin60°=，∴DH=，∴PB+PD的最小值为．故答案为：．

（3）①以A为圆心AB为半径画弧与对称轴有两个交点，以B为圆心AB为半径画弧与对称轴也有两个交点，线段AB的垂直平分线与对称轴有一个交点，所以满足条件的点M有5个，即满足条件的点N也有5个，故答案为：5．

②如图，RT△AOB中，∵tan∠ABO=，∴∠ABO=30°，作AB的中垂线与y轴交于点E，连接EA，则∠AEB=120°，以E为圆心，EB为半径作圆，与抛物线对称轴交于点F、G．

则∠AFB=∠AGB=60°，从而线段FG上的点满足题意，∵E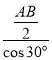B==，∴OE=OB﹣EB=，∵F（，t），，∴，解得t=或，故F（，），G（，），∴t的取值范围≤t≤