题目内容
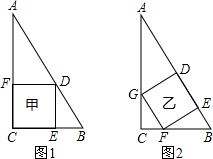
现有一块直角三角形木板，它的两条直角边分别为3米和4米．要把它加工成面积最大的正方形桌面，甲、乙二人加工方法分别如图1和图2所示．请运用所学知识说明谁的加工方法符合要求．
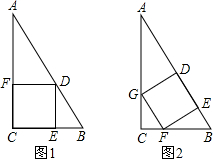
图1加工的方法合理．
设图1加工桌面长xm，
∵FD∥BC，
∴Rt△AFD∽Rt△ACB，
∴AF：AC=FD：BC，
即（4-x）：4=x：3，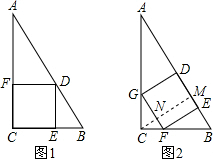
解得x=
，
设图2加工桌面长ym，过点C作CM⊥AB，垂足是M，与GF相交于点N，
∵GF∥DE，
∴△CGF∽△CAB，
∴CN：CM=GF：AB，
∴（CM-y）：CM=y：AB．
∴AB=
．
由面积相等可求得CM=2.4，
故此可求得y=
；
很明显x＞y，故x2＞y2，
∴图1加工的方法合理．
设图1加工桌面长xm，
∵FD∥BC，
∴Rt△AFD∽Rt△ACB，
∴AF：AC=FD：BC，
即（4-x）：4=x：3，
解得x=
| 12 |
| 7 |
设图2加工桌面长ym，过点C作CM⊥AB，垂足是M，与GF相交于点N，
∵GF∥DE，
∴△CGF∽△CAB，
∴CN：CM=GF：AB，
∴（CM-y）：CM=y：AB．
∴AB=
| y•CM |
| CM-y |
由面积相等可求得CM=2.4，
故此可求得y=
| 60 |
| 37 |
很明显x＞y，故x2＞y2，
∴图1加工的方法合理．
练习册系列答案
相关题目
