题目内容
【题目】如图,在□ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断线段BE、DF的关系,并证明你的结论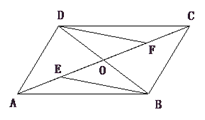
【答案】![]()
【解析】根据平行四边形的性质对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形,从而得出BE=DF,BE∥DF.
解:由题意得:BE=DF,BE∥DF.理由如下:
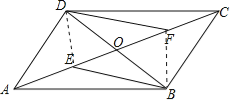
连接DE、BF.
∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE=OF,
∴BFDE是平行四边形,
∴BE=DF,BE∥DF.
本题考查了平行四边形的基本性质和判定定理的运用.性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
【题目】某校合唱团有30名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) | 13 | 14 | 15 | 16 |
频数(单位:名) | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差