ЬтФПФкШн
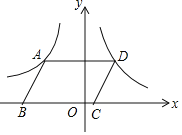
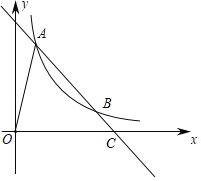
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНЃx2ЃЋbxЃЋcгывЛжБЯпЯрНЛгкA(Ѓ1ЃЌ0)ЃЌC(2ЃЌ3)СНЕуЃЌгыyжсНЛгкЕуNЃЌЦфЖЅЕуЮЊD.
(1)ЧѓХзЮяЯпМАжБЯпACЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЩшЕуM(3ЃЌm)ЃЌЧѓЪЙMNЃЋMDЕФжЕзюаЁЪБmЕФжЕЃЛ
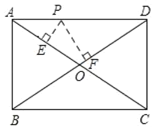
(3)ШєХзЮяЯпЕФЖдГЦжсгыжБЯпACЯрНЛгкЕуBЃЌEЮЊжБЯпACЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуEзїEFЁЮBDНЛХзЮяЯпгкЕуFЃЌвдBЃЌDЃЌEЃЌFЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊЦНааЫФБпаЮЃПШєФмЃЌЧѓЕуEЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
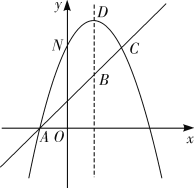
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊyЃНЃx2ЃЋ2xЃЋ3ЃЛжБЯпACЕФНтЮіЪНЮЊyЃНxЃЋ1ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉEЃЈ0ЃЌ1ЃЉЛђ
ЃЛЃЈ3ЃЉEЃЈ0ЃЌ1ЃЉЛђ Лђ
Лђ .
.
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЁЂCЕФзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУГіbЁЂcЕФжЕЃЌМЬЖјЕУГіХзЮяЯпНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіACЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉРћгУжсЖдГЦЧѓзюЖЬТЗОЖЕФжЊЪЖЃЌевЕНNЕуЙигкжБЯпx=3ЕФЖдГЦЕуNЁфЃЌСЌНгN'DЃЌN'DгыжБЯпx=3ЕФНЛЕуМДЪЧЕуMЕФЮЛжУЃЌМЬЖјЧѓГіmЕФжЕЃЎ
ЃЈ3ЃЉЩшГіЕуEЕФзјБъЃЌЗжЧщПіЬжТлЃЌЂйЕБЕуEдкЯпЖЮACЩЯЪБЃЌЕуFдкЕуEЩЯЗНЃЌЂкЕБЕуEдкЯпЖЮACЃЈЛђCAЃЉбгГЄЯпЩЯЪБЃЌЕуFдкЕуEЯТЗНЃЌИљОнЦНааЫФБпаЮЕФаджЪБэЪОГіFЕФзјБъЃЌНЋЕуFЕФзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУГіxЕФжЕЃЌМЬЖјЧѓГіЕуEЕФзјБъЃЎ
ЃЈ1ЃЉгЩХзЮяЯпy=-x2+bx+cЙ§ЕуAЃЈ-1ЃЌ0ЃЉМАCЃЈ2ЃЌ3ЃЉЃЌПЩЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЮЊy=-x2+2x+3ЃЌ
ЩшжБЯпACНтЮіЪНЮЊy=kx+nЃЌНЋЕуAЃЈ-1ЃЌ0ЃЉЁЂCЃЈ2ЃЌ3ЃЉДњШыЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪжБЯпACЮЊy=x+1ЃЎ
ЃЈ2ЃЉзїNЕуЙигкжБЯпx=3ЕФЖдГЦЕуNЁфЃЌдђNЁфЃЈ6ЃЌ3ЃЉЃЌгЩЃЈ1ЃЉЕУDЃЈ1ЃЌ4ЃЉЃЌ
ПЩЧѓГіжБЯпDNЁфЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЌ
ЃЌ
ЕБMЃЈ3ЃЌmЃЉдкжБЯпDNЁфЩЯЪБЃЌMN+MDЕФжЕзюаЁЃЌ
дђ![]() ЃЎ
ЃЎ

ЃЈ3ЃЉгЩЃЈ1ЃЉЁЂЃЈ2ЃЉЕУDЃЈ1ЃЌ4ЃЉЃЌBЃЈ1ЃЌ2ЃЉ
ЕуEдкжБЯпACЩЯЃЌЩшEЃЈxЃЌx+1ЃЉЃЌ
ЂйЕБЕуEдкЯпЖЮACЩЯЪБЃЌЕуFдкЕуEЩЯЗНЃЌдђFЃЈxЃЌx+3ЃЉЃЌ
ЁпFдкХзЮяЯпЩЯЃЌ
Ёрx+3=-x2+2x+3
НтЕУЃЌx=0Лђx=1ЃЈЩсШЅЃЉЃЌ
дђЕуEЕФзјБъЮЊЃКЃЈ0ЃЌ1ЃЉЃЎ
ЂкЕБЕуEдкЯпЖЮACЃЈЛђCAЃЉбгГЄЯпЩЯЪБЃЌЕуFдкЕуEЯТЗНЃЌдђFЃЈxЃЌx-1ЃЉЃЌ
ЁпЕуFдкХзЮяЯпЩЯЃЌ
Ёрx-1=-x2+2x+3ЃЌ
НтЕУx=![]() Лђx=
Лђx=![]() ЃЌ
ЃЌ
ЫљвдЃЌy=![]() Лђy=
Лђy=![]()
МДЕуEЕФзјБъЮЊЃКЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯПЩЕУТњзуЬѕМўЕФЕуEЮЊEЃЈ0ЃЌ1ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

 Н№ХЦНЬИЈХргХгХбЁОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ
Н№ХЦНЬИЈХргХгХбЁОэЦкФЉГхДЬ100ЗжЯЕСаД№АИЁОЬтФПЁПЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіВЛЯрЕШЧвЗЧСуЕФЪЕЪ§ИљЃЌЬНОП
гаСНИіВЛЯрЕШЧвЗЧСуЕФЪЕЪ§ИљЃЌЬНОП![]() ТњзуЕФЬѕМўЃЎ
ТњзуЕФЬѕМўЃЎ
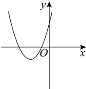
аЁЛЊИљОнбЇЯАКЏЪ§ЕФОбщЃЌШЯЮЊПЩвдДгЖўДЮКЏЪ§ЕФНЧЖШбаОПвЛдЊЖўДЮЗНГЬЕФИљЕФЗћКХЁЃЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬЃКЕквЛВНЃКЩшвЛдЊЖўДЮЗНГЬ![]() ЖдгІЕФЖўДЮКЏЪ§ЮЊ
ЖдгІЕФЖўДЮКЏЪ§ЮЊ![]() ЃЛ
ЃЛ
ЕкЖўВНЃКНшжњЖўДЮКЏЪ§ЭМЯѓЃЌПЩвдЕУЕНЯргІЕФвЛдЊЖўДЮЗНГЬжа![]() ТњзуЕФЬѕМўЃЌСаБэШчЯТБэЁЃ
ТњзуЕФЬѕМўЃЌСаБэШчЯТБэЁЃ
ЗНГЬСНИљЕФЧщПі | ЖдгІЕФЖўДЮКЏЪ§ЕФДѓжТЭМЯѓ |
|
ЗНГЬгаСНИіВЛЯрЕШЕФИКЪЕИљ |
|
|
Ђй_______ |
|
|
ЗНГЬгаСНИіВЛЯрЕШЕФе§ЪЕИљ | Ђк | Ђл____________ |
ЃЈ1ЃЉЧыНЋБэИёжаЂйЂкЂлВЙГфЭъећЃЛ
ЃЈ2ЃЉвбжЊЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЃЌШєЗНГЬЕФСНИљЖМЪЧе§Ъ§ЃЌЧѓ
ЃЌШєЗНГЬЕФСНИљЖМЪЧе§Ъ§ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.