题目内容
【题目】如图,已知BD⊥DE,CE⊥DE,垂足分别是D、E,AB=AC,∠BAC=90°,
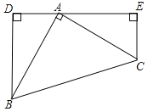
(1)△ABD≌△CAE
(2)探索DE、BD、CE长度之间的关系并证明.
【答案】(1)见解析;(2)DE=BD+CE,理由见解析
【解析】
本题证全等最主要的是找到∠DAB=∠ACE或者∠ABD=∠CAE,之后根据AAS证全等即可,而找三边关系只需要(1)问的结论,即可证明DE=BD+CE.
(1)证明:∵∠BAC=90°,
∴∠EAC+∠DAB=90°,
∵BD⊥DE,CE⊥DE,
∴∠DAB+∠DBA=90°,∠D=∠E=90°,
∴∠EAC=∠DBA,
在△ABD和△CAE中,
∵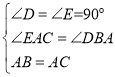
∴△ABD≌△CAE,
(2)结论:DE=BD+CE,理由如下:
∵△ABD≌△CAE,
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD.

练习册系列答案
相关题目