题目内容
【题目】 如图,点 C,F,E,B 在一条直线上, ![]() CFD =
CFD = ![]() BEA , CE = BF,DF = AE .
BEA , CE = BF,DF = AE . 
(1)求证:DF∥AE;
(2)写出 CD 与 AB 之间的关系,并证明你的结论.
【答案】
(1)证明:∵ ∠CFD=∠BEA ,
∴∠DFE=∠AEF,
∴DF∥AE.
(2)解:CD=AB,且 CD∥AB,理由如下:
∵CE = BF,
∴CE-EF=BF-EF,
即CF=BE,
在 ΔCDF 和 ΔBAE 中,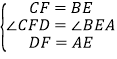
∴ΔCDF≌ΔBAE,
∴CD=BA,∠C=∠B,
∴CD∥BA.
【解析】(1)根据等角的补角相等得到∠DFE=∠AEF,再由内错角相等,两直线平行即可得证.
(2)CD=AB,且 CD∥AB,理由如下:由CE = BF得出CF=BE,再利用全等三角形的判定SAS得出ΔCDF≌ΔBAE,由全等三角形的性质得出CD=BA,
∠C=∠B,再由内错角相等,两直线平行得出CD∥BA.
【考点精析】利用对顶角和邻补角和平行线的判定对题目进行判断即可得到答案,需要熟知两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
