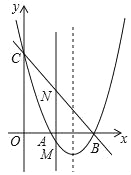
题目内容
【题目】已知,如图在平面直角坐标系中,过点A(0,2)的直线与⊙O相切于点C,与x轴交于点B且半径为![]() .
.
(1)求∠BAO的度数.(2)求直线AB的解析式.
【答案】(1)∠BAO=60°;(2)![]() .
.
【解析】
(1)连接OC,由切线的性质可知OC⊥AB且OC![]() .在Rt△AOC中,可求得sin∠BAO,则可求得∠BAO的度数;
.在Rt△AOC中,可求得sin∠BAO,则可求得∠BAO的度数;
(2)在Rt△AOB中,利用直角三角形的性质可求得BO的长,则可求得B点坐标,利用待定系数法可求得直线AB的解析式.
(1)连接OC,如图,∵AB与⊙O相切,∴OC⊥AB且OC![]() .
.
∵A(0,2),∴OA=2.在Rt△AOC中,sin∠BAO![]() ,∴∠BAO=60°;
,∴∠BAO=60°;
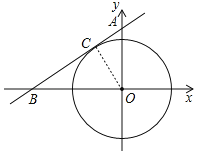
(2)∵∠BAO=60°,∴∠OBC=30°,∴OB=2OC=2![]() ,∴B(﹣2
,∴B(﹣2![]() ,0),设直线AB解析式为y=kx+b,∴
,0),设直线AB解析式为y=kx+b,∴![]() ,解得:
,解得: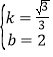 ,∴直线AB解析式为y
,∴直线AB解析式为y![]() x+2.
x+2.

 阅读快车系列答案
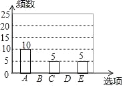
阅读快车系列答案【题目】随着移动终端设备的升级换代,手机己经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天:B.学习:C.购物:D.游戏:E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 20% |
C | 5 | 10% |
D | p | 40% |
E | 5 | 10% |
合计 | 100% |
根据以上信息解答下列问题:
(1)m= ,n= ,p= ;
(2)补全条形统计图;
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.