题目内容
如图，线段AB=8cm，C是线段AB上一点，AC=3.2cm，M是AB的中点，N是AC的中点，求线段MN的长．
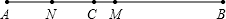
解：∵AB=8cm，M是AB的中点，
∴AM=BM=4cm
∵AC=3.2cm，N是AC的中点，
∴AN=CN=1.6cm
∴MN=AM-AN
=4-1.6
=2.4cm．
分析：先根据“M是AB的中点，N是AC的中点”求出AM、AN的长度，再利用MN=AM-AN即可求出MN的长度．
点评：本题主要考查线段中点的运用，线段的中点把线段分成两条相等的线段．
∴AM=BM=4cm
∵AC=3.2cm，N是AC的中点，
∴AN=CN=1.6cm
∴MN=AM-AN
=4-1.6
=2.4cm．
分析：先根据“M是AB的中点，N是AC的中点”求出AM、AN的长度，再利用MN=AM-AN即可求出MN的长度．
点评：本题主要考查线段中点的运用，线段的中点把线段分成两条相等的线段．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
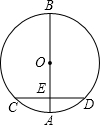如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，那么线段OE的长为（ ）| A、10 | B、8 | C、6 | D、4 |
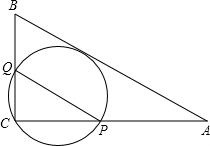如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q，则线段PQ长度的最小值是（ ）| A、4.75 | ||
| B、4.8 | ||
| C、5 | ||
D、4
|
9、如图，在△ABC中，已知∠ABC和∠ACB的平分线相交于点D，过D点作EF∥BC，交AB于点E，交AC于点F，若BE+CF=9，则线段EF的长为（ ）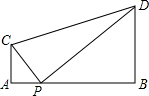
如图，AC⊥AB，BD⊥AB，AB=10，AC=2；用以个三角尺进行如下操作：将直角顶点P在线段AB上滑动，一直角边始终经过点C，另一直角边与BE相交于点D，若BD=8，则AP的长为（ ）
如图，点C，D在线段AB上，AC=