Question

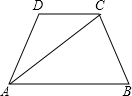
如图，等腰梯形ABCD中，AB∥CD，对角线AC垂直于一腰BC，且AC平分∠BAD，若梯形的中位线长为p，则梯形ABCD的周长为（　　）

A． 7 3 p

B．3p

C． 10 3 p

D．4p

Answer 1

∵AB∥CD
∴∠DCA=∠BAC
∵AC平分∠BAD
∴∠DAC=∠CAB
∴∠DAC=∠DCA
∴AD=DC=BC
∵∠CAB=

1

2

∠DAB=

1

2

∠B，∠ACB=90°
∴∠CAB=30°
∴AB=2BC
∵

1

2

（AB+DC）=p

1

2

（2DC+DC）=p
∴DC=

2

3

p
∵梯形ABCD的周长=AB+BC+CD+AD=5CD=

10

3

p．
故选C．