Question

【题目】如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，则sin∠ECF=（　　）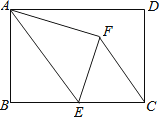

A.
B.
C.
D.

Answer 1

【答案】D
【解析】过E作EH⊥CF于H，
由折叠的性质得：BE=EF，∠BEA=∠FEA，
∵点E是BC的中点，
∴CE=BE，
∴EF=CE，
∴∠FEH=∠CEH，
∴∠AEB+∠CEH=90°，
在矩形ABCD中，
∵∠B=90°，
∴∠BAE+∠BEA=90°，
∴∠BAE=∠CEH，∠B=∠EHC，
∴△ABE∽△EHC，
∴，
∵AE==10，
∴EH=，
∴sin∠ECF==，
故选D．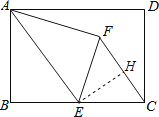

【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．