题目内容
下列四个命题，你认为正确的命题是________（只填命题的序号）
①计算
=________；
②已知x1、x2是方程x2-2x-1=0的两个根，则
=________；
③关于x的一元二次方程x2-mx+（m-2）=0有________的实数根；
④若xy＞0，且x+y＞0，那么点P（x，y）关于原点的对称点在第________象限．
①②③ 0 -2 两个不相等 二
分析：①化简二次根式；②利用根与系数的关系求值；③根据根的判别式判断实数根的情况；④先根据已知条件确定x、y的取值，然后再判断关于原点对称点的象限．
解答：
①原式=3
-4+=0，正确；
②∵x1+x2=2，x1•x2=-1，∴=
=
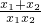=-2，正确；
③△=b2-4ac=（-m）2-4×1×（m-2）=m2-4m+8=（m-2）2+4≥0，
∴方程有两个不相等的实数根，正确；
④∵xy＞0，且x+y＞0，∴x＞0，y＞0，
∴P点关于原点对称的点在第三象限，错误．
故正确的命题有①②③．
点评：本题利用了二次根式的化简、一元二次方程根与系数的关系、根的判别式、坐标系中任意点关于原点对称的点的确定．
分析：①化简二次根式；②利用根与系数的关系求值；③根据根的判别式判断实数根的情况；④先根据已知条件确定x、y的取值，然后再判断关于原点对称点的象限．
解答：
①原式=3
-4+=0，正确；②∵x1+x2=2，x1•x2=-1，∴
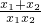===-2，正确；③△=b2-4ac=（-m）2-4×1×（m-2）=m2-4m+8=（m-2）2+4≥0，
∴方程有两个不相等的实数根，正确；
④∵xy＞0，且x+y＞0，∴x＞0，y＞0，
∴P点关于原点对称的点在第三象限，错误．
故正确的命题有①②③．
点评：本题利用了二次根式的化简、一元二次方程根与系数的关系、根的判别式、坐标系中任意点关于原点对称的点的确定．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
= ；
= ；