题目内容
在二次函数y=ax2+bx+c中，若b2=ac，且当x=0时，y=-4，则y有最分析：先根据题意判断出a的正负，再直接套用公式求其最值即可．
解答：解：∵在二次函数y=ax2+bx+c中
当x=0时，y=-4，则c=-4
∵b2=ac＞0，c=-4＜0，
∴a＜0，y有最大值
且该值为
=
=
c （1）
把c=-4代入（1）得：
=
=
c=
×（-4）=-3．
当x=0时，y=-4，则c=-4
∵b2=ac＞0，c=-4＜0，
∴a＜0，y有最大值
且该值为
| 4ac-b2 |
| 4a |
| 3ac |
| 4a |
| 3 |
| 4 |
把c=-4代入（1）得：
| 4ac-b2 |
| 4a |
| 3ac |
| 4a |
| 3 |
| 4 |
| 3 |
| 4 |
点评：本题考查的是二次函数的图象与其系数的关系及二次函数的最值问题，比较简单．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
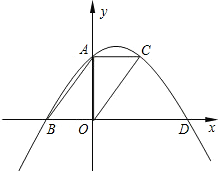如图，已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上，又点A、B分别在y轴和x轴上，∠ABO=45°．图象顶点的横坐标为2，求二次函数解析式．