题目内容
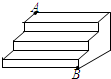如图是一个三级台阶，它的每一级的长、宽、高分别为55寸、10寸和6寸，A和B是这个台阶的两个相对端点，A点上有一只蚂蚁想到B点去吃可口的食物，则它所走的最短路线长度是（ ）| A、71寸 | B、73寸 | C、100寸 | D、103寸 |
分析：展开后得到直角三角形ACB，根据题意求出AC、BC，根据勾股定理求出AB即可．
解答：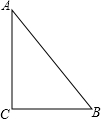
解：展开后由题意得：∠C=90°，AC=3×10+3×6=48（寸），
BC=55寸，
由勾股定理得：AB=
=
=73（寸），
故选B．
解：展开后由题意得：∠C=90°，AC=3×10+3×6=48（寸），BC=55寸，
由勾股定理得：AB=
| AC2+BC2 |
| 482+ 552 |
故选B．
点评：本题主要考查对勾股定理，平面展开-最短路径问题等知识点的理解和掌握，能理解题意知道是求出直角三角形ABC的斜边AB的长是解此题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
12、如图是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm．A和B是这个台阶上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为
16、如图是一个三级台阶，它的每一级长、宽、高分别是2米、0.3米、0.2米，A，B是这个台阶上两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿台阶面爬行到B点最短路程是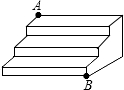
如图是一个三级台阶，它的每一级的长、宽、高分别为7寸、5寸和3寸，A和B是这个台阶的两个相对端点，A点上有一只蚂蚁想到B点去吃可口的食物，则它所走的最短路线长度是
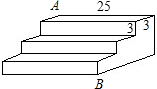如图是一个三级台阶，它的每一级的长、宽和高分别为25dm、3dm、3dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到 B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是