Question

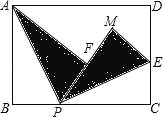
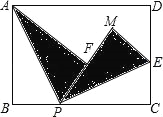
【题目】如图，矩形纸片ABCD的边AB=3，BC=4，点P是BC边上一动点（不与B、C重合），现将△ABP沿AP翻折，得到△AFP，再在CD边上选择适当的点E，将△PCE沿PE翻折，得到△PME，且直线PF、PM重合，若点F落在矩形纸片的内部，则CE的最大值是 ．

Answer 1

【答案】

【解析】

试题分析：设CE=y，PB=x，由△ABP∽△PCE，得：，由此构建二次函数，利用二次函数的性质解决问题． 设CE=y，PB=x，∵∠APB=∠APF，∠EPF=∠EPC， ∵2∠APF+2∠EPF=180°，

∴∠APF+∠EPF=90°， ∴∠APE=90°， ∴∠APB+∠CPE=90°，∠CPE+∠PEC=90°，

∴∠APB=∠PEC，∵∠B=∠C=90°， ∴△ABP∽△PCE， ∴， ∴，

∴y=﹣（x2﹣4x）=﹣（x﹣2）2+， ∴x=2时，y有最大值，最大值为．