Question

【题目】（1）如图1已知：∠B=25°，∠BED=80°，∠D=55°．探究AB与CD有怎样的位置关系.

（2）如图2已知AB∥EF，试猜想∠B，∠F，∠BCF之间的关系，写出这种关系，并加以证明.

（3）如图3已知AB∥CD，试猜想∠1，∠2，∠3，∠4，∠5之间的关系，请直接写出这种关系，不用证明.

Answer 1

【答案】（1）详见解析（2）∠BCF=∠B+∠F（3）∠1+∠3+∠5=∠2+∠4

【解析】

（1）过点E作EF∥AB，得∠BEF =25°，得∠DEF=55°，从而可证AB∥CD；

（2）作CD∥AB，根据平行线的传递性得CD∥EF，则根据平行线的性质得∠BCD=∠B，∠DCF=∠F，所以∠BCD+∠DCF=∠B+∠F，故可得结论；

（3）方法同（2）

（1）过点E作EF∥AB

∵∠B=25°

∴∠BEF=∠B=25°

∵∠BED=80°

∴∠DEF=∠BED－∠BEF=55°

∵∠D=55°

∴∠D=∠DEF

∴EF∥CD

∴AB∥CD

（2）过点C作CD∥AB，则CD∥EF，

∵AB∥CD，

∴∠BCD=∠B，

∵CD∥EF，

∴∠DCF=∠F，

∴∠BCD+∠DCF=∠B+∠F，

即∠C=∠B+∠F．

（3）∠1+∠3+∠5=∠2+∠4，

如图，

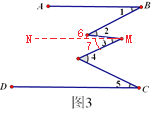
作MN∥AB，

由（2）的结论得到∠2=∠1+∠6，∠4=∠5+∠7，

∴∠2+∠4=∠1+∠6+∠5+∠7=∠1+∠3+∠5.