题目内容
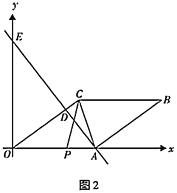
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.

(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
【答案】(1)![]()
(2)12
(3)相似三角形的基本知识推出该角度的相等,不能
【解析】
试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为![]() 。
。
又∵二次函数图象经过原点(0,0),∴![]() ,解得
,解得![]() 。
。
∴二次函数的关系式为![]() ,即
,即![]() 。(2分)
。(2分)
(2)设直线OA的解析式为![]() ,将A(6,-3)代入得
,将A(6,-3)代入得![]() ,解得
,解得![]() 。
。
∴直线OA的解析式为![]() 。
。
把x=4代入![]() 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。
又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴![]() 。(3分)
。(3分)
(3)①证明:过点A作AH⊥![]() 于点H,,
于点H,,![]() 与x轴交于点D。则
与x轴交于点D。则
设A(![]() ),
),
则直线OA的解析式为 。
。
则M(![]() ),N(
),N(![]() ),H(
),H(![]() )。
)。
∴OD=4,ND=![]() ,HA=
,HA=![]() ,NH=
,NH=![]() 。
。
∴ 。
。
∴![]()
![]() 。∴∠AM=∠ONM。(2分)
。∴∠AM=∠ONM。(2分)
②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则![]() 。
。
∵![]() ,
,
∴![]() 。
。
整理,得![]() ,解得
,解得![]() ,
,![]() 。
。
∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴![]() 。
。
∵OD=4,MD=![]() ,ND=
,ND=![]() ,∴
,∴![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴![]() 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)

【题目】某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票用时,单位:分),得到如下表所示的频数分布表.
分组 | 频数 | |
一组 | 0≤t<5 | 0 |
二组 | 5≤t<10 | 10 |
三组 | 10≤t<15 | 10 |
四组 | 15≤t<20 | |
五组 | 20≤t<25 | 30 |
合计 | 100 | |
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)旅客购票用时的平均数可能落在哪一小组内?
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么请你决策一下至少要增加几个窗口?
【题目】甲、乙两班举行电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表:
输入汉字个数(个) | 132 | 133 | 134 | 135 | 136 | 137 | ||
甲班人数人) | 1 | 0 | 2 | 4 | 1 | 2 | ||
乙班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 | ||
请分别判断下列同学是说法是否正确,并说明理由.
(1)两个班级输入汉字个数的平均数相同;
(2)两个班学生输入汉字的中位数相同众数也相同;
(3)甲班学生比乙班学生的成绩稳定.