题目内容
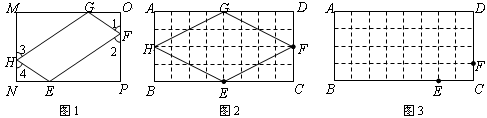
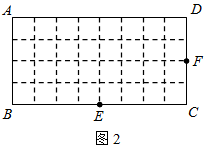
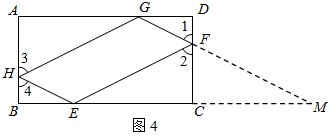
如图1,矩形MNPQ中,点E、F、G、H分别在NP、PQ、QM、MN上,若∠1=∠2=∠3=∠4,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且AB=4,BC=8.
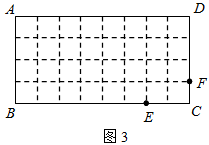
(1)在图2、图3中,点E、F分别在BC、CD边上,图2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
(2)图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少;
(3)图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的面积各是多少.
【答案】分析:(1)根据网格结构,作出相等的角即可得到反射四边形;
(2)图2中,利用勾股定理求出EF=FG=GH=HE的长度,然后即可得到周长,图3中利用勾股定理求出EF=GH,FG=HE的长度,然后求出周长,从而得到四边形EFGH的周长是定值;
(3)根据网格得出各四边形的面积,进而得出答案.
解答: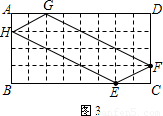 解:(1)如图3所示:
解:(1)如图3所示:
利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH.
(2)∵图2中HE=2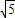 ,EF=2
,EF=2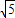 ,GF=2
,GF=2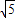 ,HG=2
,HG=2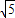 ,
,
∴四边形EFGH的周长为:2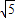 ×4=8
×4=8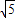 ,
,
图3中HE=3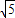 ,EF=
,EF=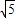 ,GF=3
,GF=3 ,HG=
,HG=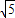 ,
,
∴四边形EFGH的周长为:(3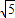 +
+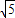 )×2=8
)×2=8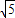 ,
,
∴图2、图3中矩形ABCD的反射四边形EFGH的周长是定值,定值是 .
.
(3)∵图2中四边形EFGH的面积为:4×8- ×2×4×4=16,
×2×4×4=16,
图3中四边形EFGH的面积为:4×8- ×1×2×2-
×1×2×2- ×3×6×2=12,
×3×6×2=12,
∴图2、图3中矩形ABCD的反射四边形EFGH的面积不是定值,它们的面积分别是16、12.
点评:本题考查了应用与设计作图、勾股定理的应用、矩形的性质等知识,读懂题意理解“反射四边形EFGH”特征是解题的关键.
(2)图2中,利用勾股定理求出EF=FG=GH=HE的长度,然后即可得到周长,图3中利用勾股定理求出EF=GH,FG=HE的长度,然后求出周长,从而得到四边形EFGH的周长是定值;
(3)根据网格得出各四边形的面积,进而得出答案.
解答:
 解:(1)如图3所示:
解:(1)如图3所示:利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH.
(2)∵图2中HE=2
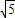 ,EF=2
,EF=2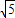 ,GF=2
,GF=2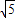 ,HG=2
,HG=2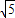 ,
,∴四边形EFGH的周长为:2
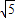 ×4=8
×4=8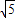 ,
,图3中HE=3
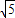 ,EF=
,EF=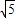 ,GF=3
,GF=3 ,HG=
,HG=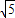 ,
,∴四边形EFGH的周长为:(3
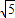 +
+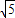 )×2=8
)×2=8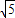 ,
,∴图2、图3中矩形ABCD的反射四边形EFGH的周长是定值,定值是
 .
.(3)∵图2中四边形EFGH的面积为:4×8-
 ×2×4×4=16,
×2×4×4=16,图3中四边形EFGH的面积为:4×8-
 ×1×2×2-
×1×2×2- ×3×6×2=12,
×3×6×2=12,∴图2、图3中矩形ABCD的反射四边形EFGH的面积不是定值,它们的面积分别是16、12.
点评:本题考查了应用与设计作图、勾股定理的应用、矩形的性质等知识,读懂题意理解“反射四边形EFGH”特征是解题的关键.

练习册系列答案
相关题目

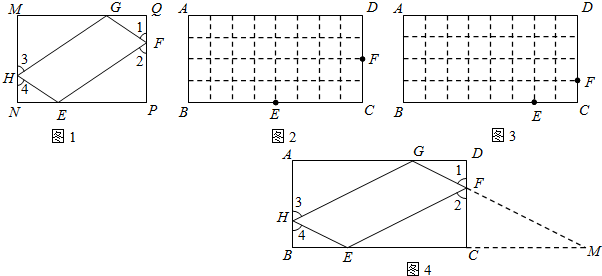
 如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,
如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,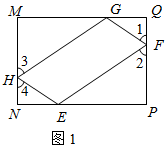
 ,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且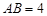 ,
,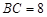 .
.