题目内容
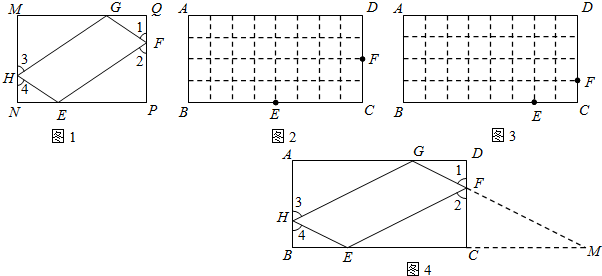
(2012•咸宁)如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若∠1=∠2=∠3=∠4,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且AB=4,BC=8.
理解与作图:
(1)在图2,图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.
理解与作图:
(1)在图2,图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.

分析:(1)根据网格结构,作出相等的角即可得到反射四边形;
(2)图2中,利用勾股定理求出EF=FG=GH=HE的长度,然后即可得到周长,图3中利用勾股定理求出EF=GH,FG=HE的长度,然后求出周长,从而得到四边形EFGH的周长是定值;
(3)证法一:延长GH交CB的延长线于点N,再利用“角边角”证明Rt△FCE和Rt△FCM全等,根据全等三角形对应边相等可得EF=MF,EC=MC,同理求出NH=EH,NB=EB,从而得到MN=2BC,再证明GM=GN,过点G作GK⊥BC于K,根据等腰三角形三线合一的性质求出MK=
MN=8,再利用勾股定理求出GM的长度,然后即可求出四边形EFGH的周长;
证法二:利用“角边角”证明Rt△FCE和Rt△FCM全等,根据全等三角形对应边相等可得EF=MF,EC=MC,再根据角的关系推出∠M=∠HEB,根据同位角相等,两直线平行可得HE∥GF,同理可证GH∥EF,所以四边形EFGH是平行四边形,过点G作GK⊥BC于K,根据边的关系推出MK=BC,再利用勾股定理列式求出GM的长度,然后即可求出四边形EFGH的周长.
(2)图2中,利用勾股定理求出EF=FG=GH=HE的长度,然后即可得到周长,图3中利用勾股定理求出EF=GH,FG=HE的长度,然后求出周长,从而得到四边形EFGH的周长是定值;
(3)证法一:延长GH交CB的延长线于点N,再利用“角边角”证明Rt△FCE和Rt△FCM全等,根据全等三角形对应边相等可得EF=MF,EC=MC,同理求出NH=EH,NB=EB,从而得到MN=2BC,再证明GM=GN,过点G作GK⊥BC于K,根据等腰三角形三线合一的性质求出MK=
| 1 |
| 2 |
证法二:利用“角边角”证明Rt△FCE和Rt△FCM全等,根据全等三角形对应边相等可得EF=MF,EC=MC,再根据角的关系推出∠M=∠HEB,根据同位角相等,两直线平行可得HE∥GF,同理可证GH∥EF,所以四边形EFGH是平行四边形,过点G作GK⊥BC于K,根据边的关系推出MK=BC,再利用勾股定理列式求出GM的长度,然后即可求出四边形EFGH的周长.
解答:解:(1)作图如下:(2分)
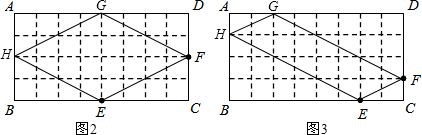
(2)在图2中,EF=FG=GH=HE=
=
=2
,
∴四边形EFGH的周长为4×2
=8
,(3分)
在图3中,EF=GH=
=
,FG=HE=
=
=3
,
∴四边形EFGH的周长为2×
+2×3
=2
+6
=8
.(4分)
猜想:矩形ABCD的反射四边形的周长为定值.(5分)
(3)证法一:延长GH交CB的延长线于点N.
∵∠1=∠2,∠1=∠5,
∴∠2=∠5.
而FC=FC,
∴Rt△FCE≌Rt△FCM.
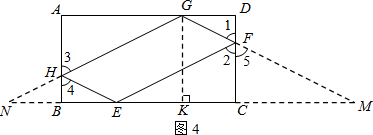
∴EF=MF,EC=MC,(6分)
同理:NH=EH,NB=EB.
∴MN=2BC=16.(7分)
∵∠M=90°-∠5=90°-∠1,∠N=90°-∠3,
∴∠M=∠N.∴GM=GN.(8分)
过点G作GK⊥BC于K,则KM=
MN=8,(9分)
∴GM=
=
=4
,
∴四边形EFGH的周长为2GM=8
,(10分)
证法二:∵∠1=∠2,∠1=∠5,
∴∠2=∠5.
而FC=FC,
∴Rt△FCE≌Rt△FCM.
∴EF=MF,EC=MC.(6分)
∵∠M=90°-∠5=90°-∠1,∠HEB=90°-∠4,
而∠1=∠4,
∴∠M=∠HEB.
∴HE∥GF.
同理:GH∥EF.
∴四边形EFGH是平行四边形.(7分)
∴FG=HE,
而∠1=∠4,
∴Rt△FDG≌Rt△HBE.
∴DG=BE.(8分)
过点G作GK⊥BC于K,则KM=KC+CM=GD+CM=BE+EC=8.(9分)
∴GM=
=
=4
,
∴四边形EFGH的周长为2GM=8
.(10分)

(2)在图2中,EF=FG=GH=HE=
| 22+42 |
| 20 |
| 5 |
∴四边形EFGH的周长为4×2
| 5 |
| 5 |
在图3中,EF=GH=
| 22+12 |
| 5 |
| 32+62 |
| 45 |
| 5 |
∴四边形EFGH的周长为2×
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
猜想:矩形ABCD的反射四边形的周长为定值.(5分)
(3)证法一:延长GH交CB的延长线于点N.
∵∠1=∠2,∠1=∠5,
∴∠2=∠5.
而FC=FC,
∴Rt△FCE≌Rt△FCM.

∴EF=MF,EC=MC,(6分)
同理:NH=EH,NB=EB.
∴MN=2BC=16.(7分)
∵∠M=90°-∠5=90°-∠1,∠N=90°-∠3,
∴∠M=∠N.∴GM=GN.(8分)
过点G作GK⊥BC于K,则KM=
| 1 |
| 2 |
∴GM=
| GK2+KM2 |
| 42+82 |
| 5 |
∴四边形EFGH的周长为2GM=8
| 5 |
证法二:∵∠1=∠2,∠1=∠5,
∴∠2=∠5.
而FC=FC,
∴Rt△FCE≌Rt△FCM.
∴EF=MF,EC=MC.(6分)
∵∠M=90°-∠5=90°-∠1,∠HEB=90°-∠4,
而∠1=∠4,
∴∠M=∠HEB.
∴HE∥GF.
同理:GH∥EF.
∴四边形EFGH是平行四边形.(7分)
∴FG=HE,
而∠1=∠4,
∴Rt△FDG≌Rt△HBE.
∴DG=BE.(8分)
过点G作GK⊥BC于K,则KM=KC+CM=GD+CM=BE+EC=8.(9分)
∴GM=
| GK2+KM2 |
| 42+82 |
| 5 |
∴四边形EFGH的周长为2GM=8
| 5 |
点评:本题考查了应用与设计作图,全等三角形的判定与性质,勾股定理的应用,矩形的性质,读懂题意理解“反射四边形EFGH”特征是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 (2012•咸宁)如图,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC且交CD于E,E为CD的中点,EF∥BC交AB于F,EG∥AB交BC于G,当AD=2,BC=12时,四边形BGEF的周长为
(2012•咸宁)如图,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC且交CD于E,E为CD的中点,EF∥BC交AB于F,EG∥AB交BC于G,当AD=2,BC=12时,四边形BGEF的周长为 转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒. (2012•咸宁)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是
(2012•咸宁)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是 (2012•咸宁)如图,一次函数y1=kx+b的图象与反比例函数
(2012•咸宁)如图,一次函数y1=kx+b的图象与反比例函数 (2012•咸宁)如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF∥CD,连接BC.
(2012•咸宁)如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF∥CD,连接BC.