题目内容
 如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,
如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,(1)当x=3时,y=
9
9
;当x=12时,y=6
6
;当y=6时,x=2或12
2或12
;(2)分别求当0<x<4、4≤x≤10、10<x<14时,y与x的函数关系式.
分析:(1)利用当x=3时,y=
MN×RN,当x=12时,y=
RM×MN以及当y=6时分别求出即可;
(2)利用当0<x<4、4≤x≤10、10<x<14时根据R不同的位置,分别求出y与x的函数关系式即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用当0<x<4、4≤x≤10、10<x<14时根据R不同的位置,分别求出y与x的函数关系式即可.
解答: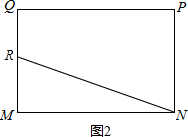
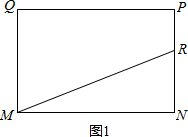 解:(1)如图1,∵点R运动的路程为x,△MNR的面积为y,
解:(1)如图1,∵点R运动的路程为x,△MNR的面积为y,
∴当x=3时,y=
MN×RN=
×6×3=9,
如图2,当x=12时,y=
RM×MN=
×2×6=6,
根据以上计算可以得出当y=6时,x=2或12,
故答案为:9,6,2或12;
(2)当0≤x<4时,R在PN上运动,y=
MN×RN=
×6×x=3x;
当4≤x≤10时,R在QP上运动,y=
MN×PN=
×6×4=12;
当10<x≤14时,R在QM上运动,y=
MN×RM=
×6×[4-(x-10)]=42-3x.

 解:(1)如图1,∵点R运动的路程为x,△MNR的面积为y,
解:(1)如图1,∵点R运动的路程为x,△MNR的面积为y,∴当x=3时,y=
| 1 |
| 2 |
| 1 |
| 2 |
如图2,当x=12时,y=
| 1 |
| 2 |
| 1 |
| 2 |
根据以上计算可以得出当y=6时,x=2或12,
故答案为:9,6,2或12;
(2)当0≤x<4时,R在PN上运动,y=
| 1 |
| 2 |
| 1 |
| 2 |
当4≤x≤10时,R在QP上运动,y=
| 1 |
| 2 |
| 1 |
| 2 |
当10<x≤14时,R在QM上运动,y=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了三角形的面积以及矩形的性质和分段函数等知识,利用R位置的不同得出y与x之间的关系是解题关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目

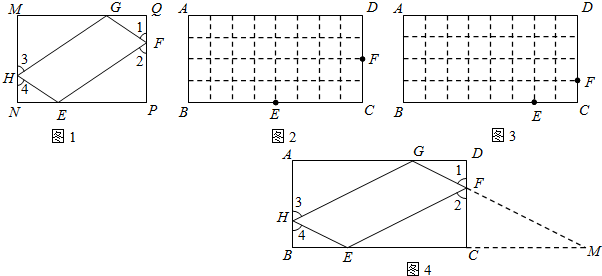
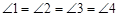 ,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且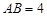 ,
, .
.
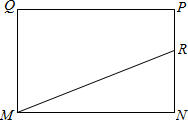 如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,
如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,