题目内容
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;①AD平分∠BAC;③AE=AD;④AB+AC=2AE.其中正确的有( ).
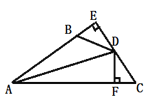
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据HL定理证明Rt△BDE≌Rt△CDF得出对应边DE=DF,进一步得出AD平分∠BAC,①②正确;再根据直角三角形斜边大于直角边得出AE>AD,③错误;最后利用全等三角形性质进一步证明④即可.
∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
在Rt△BDE与Rt△CDF中,
∵BD=CD,BE=CF
∴Rt△BDE≌Rt△CDF,
∴DE=DF,即①正确,
又∵∠E=∠DFC=90°,
∴AD平分∠BAC,即②正确,
在Rt△AED中,
∵AE为直角边,AD为斜边,
∴AE>AD,即③错误,
在Rt△ADE与Rt△ADF中,
∵DE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF,
∴AE=AF,
∵BE=CF,
∴AB+AC=AB+AF+CF= AB+AF+BE=AE+AF=2AE,即④正确,
综上所述,共有三个正确,
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目