题目内容
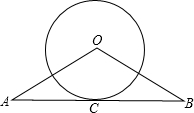 已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.(1)直线AB是⊙O的切线吗?请说明理由;
(2)若⊙O的直径为8cm,AB=10cm,求OA的长.(结果保留根号)
分析:(1)直线AB是⊙O的切线,连接OC,然后利用等腰三角形的性质即可证明OC⊥AB,接着利用切线的判定定理即可求解;
(2)根据切线的性质得到△OAC是直角三角形,同时C是AB的中点,然后利用勾股定理计算即可求解.
(2)根据切线的性质得到△OAC是直角三角形,同时C是AB的中点,然后利用勾股定理计算即可求解.
解答: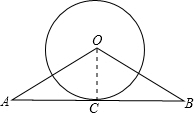 解:(1)直线AB是⊙O的切线.理由如下:
解:(1)直线AB是⊙O的切线.理由如下:
如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB于C,
∴直线AB是⊙O的切线;
(2)∵OA=OB,CA=CB,
而⊙O的直径为8cm,AB=10cm
∴OC=4,AC=5,
∴AO=
=
cm.
 解:(1)直线AB是⊙O的切线.理由如下:
解:(1)直线AB是⊙O的切线.理由如下:如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB于C,
∴直线AB是⊙O的切线;
(2)∵OA=OB,CA=CB,
而⊙O的直径为8cm,AB=10cm
∴OC=4,AC=5,
∴AO=
| OC2+AC2 |
| 41 |
点评:此题主要考查了切线的性质与判定,首先利用切线的判定定理证明切线,然后利用切线的性质和勾股定理计算即可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
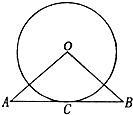 20、如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,那么直线AB是⊙O的切线吗?为什么?
20、如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,那么直线AB是⊙O的切线吗?为什么? 如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.