题目内容
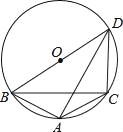
【题目】如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,求弦DC的长.
【答案】![]()
【解析】
根据直径所对的圆周角是直角,可得∠BAD=∠BCD=90°;然后求出∠CAD=30°,利用同弧所对的圆周角相等,求出∠CBD=∠CAD=30°;根据圆内接四边形对角互补,求出∠BDC=60°;再根据等弦所对的圆周角相等,求出∠ADB=∠ADC,从而求出∠ADB=30°;解直角三角形求出BD;再根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=∠BDC=![]() ×60°=30°,
×60°=30°,
在Rt△ABD中,AB=![]() AD=
AD=![]() ×6=2
×6=2![]() ,BD=2AB=4
,BD=2AB=4![]() ,
,
在Rt△BCD中,CD=![]() BD=2
BD=2![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.