题目内容
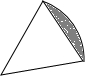
如图所示,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC.
(1)求被剪掉的扇形部分的面积;
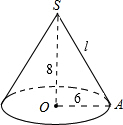
(2)用剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)

(1)求被剪掉的扇形部分的面积;
(2)用剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)

(1)连接BC,AO,
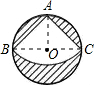
∵∠BAC=90°,OB=OC,
∴BC是圆0的直径,AO⊥BC,
∵圆的直径为1,
∴AO=OC=
,
则AC=
=
m,
故S扇形=
=
.
(2)弧BC的长l=
=
πm,
则2πR=
π,
解得:R=
.
故该圆锥的底面圆的半径是
m.

∵∠BAC=90°,OB=OC,
∴BC是圆0的直径,AO⊥BC,
∵圆的直径为1,
∴AO=OC=
| 1 |
| 2 |
则AC=
| AO2+OC2 |
| ||
| 2 |
故S扇形=
90π×(
| ||||
| 360 |
| π |
| 8 |
(2)弧BC的长l=
90π×
| ||||
| 180 |
| ||
| 4 |
则2πR=
| ||
| 4 |
解得:R=
| ||
| 8 |
故该圆锥的底面圆的半径是
| ||
| 8 |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目