题目内容
△ABC的三边长为a，b，c．它的内切圆半径为r，则△ABC的面积为
- A.（a+b+c）r
- B.
（a+b+c）r - C.2（a+b+c）r
- D.无法确定
B
分析：首先根据题意画出图，观察发现三角形ABC的内切圆半径，恰好是三角形ABC内三个三角形的高，因而可以通过面积S△ABC=S△AOB+S△BOC+S△AOC来计算．
解答：
解：S△ABC=S△AOB+S△BOC+S△AOC=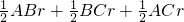
=
=
，
故选B．
点评：本题考查三角形的内切圆与内心．解决本题的关键是将求△ABC转化为求S△AOB、S△BOC、S△AOC．
分析：首先根据题意画出图，观察发现三角形ABC的内切圆半径，恰好是三角形ABC内三个三角形的高，因而可以通过面积S△ABC=S△AOB+S△BOC+S△AOC来计算．
解答：
解：S△ABC=S△AOB+S△BOC+S△AOC=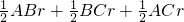==，故选B．
点评：本题考查三角形的内切圆与内心．解决本题的关键是将求△ABC转化为求S△AOB、S△BOC、S△AOC．
练习册系列答案
阅读快车系列答案
相关题目
△ABC的三边长为a，b，c．它的内切圆半径为r，则△ABC的面积为（ ）
| A、（a+b+c）r | ||
B、
| ||
| C、2（a+b+c）r | ||
| D、无法确定 |