Question

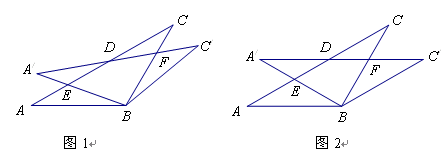
如图，在△ABC中，∠ABC=90°，∠A=30°，把△ABC绕点C旋转一定角度后得到△DEC，点A、C、E在同一直线上，则这个旋转角度为（   ）．

A．60°                     B．90°
C．120°                        D．150°

Answer 1

C

试题分析：由△ABC绕点C旋转一定角度后得到△DEC，根据旋转的性质得到∠BCE等于旋转角，由∠ABC=90°，∠A=30°，根据三角形的内角和为180°可得∠ACB的度数，再根据邻补角的定义即可求得结果。
∵∠ABC=90°，∠A=30°，
∴∠ACB=180°-∠ABC-∠A=60°，
∴∠BCE=180°-∠ACB=120°，
∴旋转角度为120°，
故选C.
点评：解答本题的关键是掌握旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心连线段的夹角等于旋转角，即可完成．