题目内容
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E. 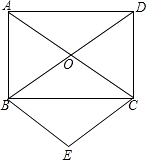
(1)求AB,AC的长;
(2)判断四边形BOCE的形状.
【答案】
(1)解:∵四边形ABCD是矩形,
∴∠ABC=90°,且∠ACB=30°,
∴AC=2AB,
设AB=x,则AC=2x,在Rt△ABCD中,由勾股定理可得x2+32=(2x)2,解得x= ![]() 或x=﹣
或x=﹣ ![]() (舍去),
(舍去),
∴AB= ![]() ,AC=2
,AC=2 ![]()
(2)解:四边形BOCE是菱形,理由如下:
∵BE∥AC,CE∥BD,
∴四边形BOCE是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴BO=CO,
∴四边形BOCE是菱形
【解析】(1)由矩形的性质可△ABC为直角三角形,由条件结合勾股定理可求得AB、AC的长;(2)由条件可先判定四边形BOCE为平行四边形,再结合矩形的性质可判定其为菱形.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目