题目内容
【题目】已知抛物线y=kx2+(k﹣2)x﹣2(其中k>0).
(1)求该抛物线与x轴的交点及顶点的坐标(可以用含k的代数式表示);
(2)若记该抛物线顶点的坐标为P(m,n),直接写出|n|的最小值;
(3)将该抛物线先向右平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
【答案】(1)抛物线的顶点坐标是(![]() ,﹣
,﹣![]() );(2)当k=2时,|n|的最小值是2;(3)新函数的解析式为y=﹣
);(2)当k=2时,|n|的最小值是2;(3)新函数的解析式为y=﹣![]() ﹣1.
﹣1.
【解析】试题分析:(1)令y=0,解方程kx2+(k﹣2)x﹣2=0即可得到抛物线与x轴的交点,根据抛物线的顶点坐标公式(﹣![]() )代入进行计算即可求解;
)代入进行计算即可求解;
(2)根据(1)的结果,然后利用绝对值的性质,再根据不等式的性质进行解答;
(3)根据左加右减,上加下减,写出平移后的抛物线顶点坐标,然后消掉字母k即可得解.
试题解析:解:(1)当y=0时,kx2+(k﹣2)x﹣2=0,即(kx﹣2)(x+1)=0,解得:x1=![]() ,x2=﹣1,∴抛物线与x轴的交点坐标是(
,x2=﹣1,∴抛物线与x轴的交点坐标是(![]() ,0)与(﹣1,0),﹣
,0)与(﹣1,0),﹣![]() =﹣
=﹣![]() =
=![]() ﹣
﹣![]() =
=![]() =﹣
=﹣![]() ,∴抛物线的顶点坐标是(
,∴抛物线的顶点坐标是(![]() ﹣
﹣![]() ,﹣
,﹣![]() );
);
(2)根据(1),|n|=|﹣![]() |=
|=![]() =
=![]() =
=![]() +
+![]() +1≥2
+1≥2![]() +1=1+1=2,当且仅当
+1=1+1=2,当且仅当![]() =
=![]() ,即k=2时取等号,∴当k=2时,|n|的最小值是2;
,即k=2时取等号,∴当k=2时,|n|的最小值是2;
(3)![]() ﹣
﹣![]() +
+![]() =
=![]() ,﹣
,﹣![]() +
+![]() =
=![]() =
=![]() =﹣
=﹣![]() k﹣1,设平移后的抛物线的顶点坐标为(x,y),则
k﹣1,设平移后的抛物线的顶点坐标为(x,y),则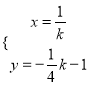 ,消掉字母k得:y=﹣
,消掉字母k得:y=﹣![]() ﹣1,∴新函数的解析式为y=﹣
﹣1,∴新函数的解析式为y=﹣![]() ﹣1.
﹣1.

练习册系列答案
相关题目