题目内容
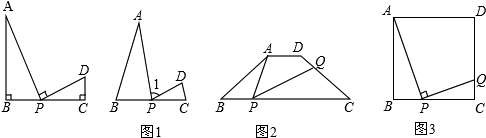
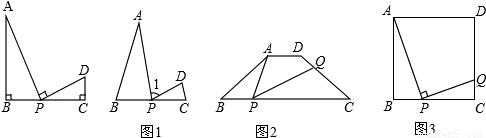
如下图1，点E是线段BC的中点，分别以B，C为直角顶点的△EAB和△EDC均是等腰直角三角形，且在BC的同侧．
(1)AE和ED的数量关系为________，AE和ED的位置关系为________；
(2)在图1中，以点E为位似中心，作△EGF与△EAB位似，点H是BC所在直线上的一点，连接GH，HD，分别得到了图2和图3；
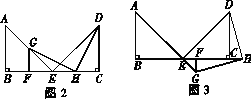
①在图2中，点F在BE上，△EGF与△EAB的相似比是1∶2，H是EC的中点．求证：GH＝HD，GH⊥HD．
②在图3中，点F在BE的延长线上，△EGF与△EAB的相似比是k∶1，若BC＝2，请直接写出CH的长为多少时，恰好使得GH＝HD且GH⊥HD(用含k的代数式表示)．
答案：
解析：
解析：
解：(1)
；2分
(2)①证明：由题意，
位似且相似比是
，
．
；5分
又
．
；7分
②
的长为
；9分
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
