��Ŀ����
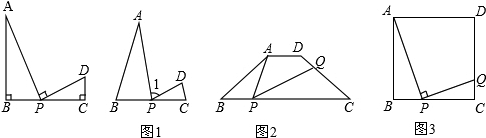
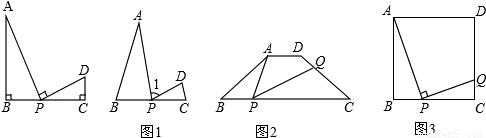
����ģ������ͼ����B��P��C��ͬһֱ���ϣ�����B=��1=��C=90�㣬���ABP�ס�PCD������
��1��ģ����չ
��ͼ1����B��P��C��ͬһֱ���ϣ�����B=��1=��C�����ABP�ס�PCD������Ϊʲô��
��2��ģ��Ӧ��
����ͼ2���ڵ�������ABCD�У�AD��BC��AD=1��AB=2��BC=4����BC�Ͻ�ȡBP=AD������APQ=��B��PQ��CD�ڵ�Q����CQ�ij���
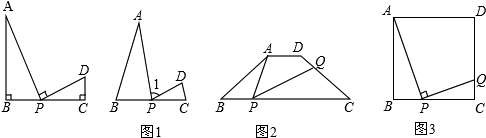
����ͼ3��������ABCD�ı߳�Ϊ1����P���߶�BC�ϵĶ��㣬����APQ=90�㣬PQ��CD��Q����P�ںδ�ʱ���߶�CQ�����Ƕ��٣�
��������1���ɡ�A=180��-����B+��APB���͡�CPD=180��-����1+��APB�����ɵó���B=��1�����A=��CPD���Ӷ�֤����ABP�ס�PCD��
��2�������ı���ABCD�ǵ������Σ����B=��C����B=��APQ=��C�����ɣ�1��֪����ABP�ס�PCD���Ӷ��ó�CQ��
����BP=x��CQ=y���ɡ�B=��APQ=90�㣬���ABP�ס�PCQ���������������ε����ʣ��ó�y��x֮��ĺ�����ϵʽ����y=-x2+x=-��x-
��2+
�����ݶ��κ��������ʵó��𰸣�
��2�������ı���ABCD�ǵ������Σ����B=��C����B=��APQ=��C�����ɣ�1��֪����ABP�ס�PCD���Ӷ��ó�CQ��
����BP=x��CQ=y���ɡ�B=��APQ=90�㣬���ABP�ס�PCQ���������������ε����ʣ��ó�y��x֮��ĺ�����ϵʽ����y=-x2+x=-��x-
| 1 |
| 2 |
| 1 |
| 4 |
����⣺��1��������
�ߡ�A=180��-����B+��APB����
��CPD=180��-����1+��APB����
��B=��1��
���A=��CPD��
�ߡ�B=��C��
���ABP�ס�PCD��
��2���١��ı���ABCD�ǵ������Σ�
���B=��C��
�ߡ�B=��APQ��
���B=��APQ=��C��
�ɣ�1��֪����ABP�ס�PCD��
��
=
��
��
=
��
��CQ=
��
����BP=x��CQ=y��
�ߡ�B=��APQ=90�㣬
���ABP�ס�PCQ��
��
=
����
=
��
��y=-x2+x=-��x-
��2+
��
�൱x=
ʱ��y���=
��
����P��BC���е�ʱ��CQ����Ϊ
��
�ߡ�A=180��-����B+��APB����
��CPD=180��-����1+��APB����
��B=��1��
���A=��CPD��
�ߡ�B=��C��
���ABP�ס�PCD��
��2���١��ı���ABCD�ǵ������Σ�
���B=��C��
�ߡ�B=��APQ��
���B=��APQ=��C��
�ɣ�1��֪����ABP�ס�PCD��
��
| CQ |
| BP |
| PC |
| AB |
��
| CQ |
| 1 |
| 3 |
| 2 |
��CQ=
| 3 |
| 2 |
����BP=x��CQ=y��
�ߡ�B=��APQ=90�㣬
���ABP�ס�PCQ��
��
| CQ |
| BP |
| PC |
| AB |
| y |
| x |
| 1-x |
| 1 |
��y=-x2+x=-��x-
| 1 |
| 2 |
| 1 |
| 4 |
�൱x=
| 1 |
| 2 |
| 1 |
| 4 |
����P��BC���е�ʱ��CQ����Ϊ
| 1 |
| 4 |
���������⿼�������������ε��ж������ʡ����κ�������ֵ���⡢�����ε������Լ����������ε����ʣ���һ���ۺ��⣬�ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ