题目内容
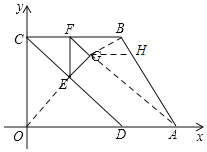
【题目】如图,四边形OABC的顶点A、C分别在x、y轴的正半抽上,点D是OA上的一点,OC=OD=4,OA=6,点B的坐标为(4,4).动点E从点C出发,以每秒![]() 个单位长度的速度沿线段CD向点D运动,过点E作BC的垂线EF交线段BC于点F,以线段EF为斜边向右作等腰直角△EFG.设点E的运动时间为t秒(0≤t≤4).
个单位长度的速度沿线段CD向点D运动,过点E作BC的垂线EF交线段BC于点F,以线段EF为斜边向右作等腰直角△EFG.设点E的运动时间为t秒(0≤t≤4).

(1)点G的坐标为( , )(用含t的代数式表示)
(2)连接OE、BG,当t为何值时,以O、C、E为顶点的三角形与△BFG相似?
(3)设点E从点C出发时,点E、F、G都与点C重合,点E在运动过程中,当△ABG 的面积为![]() 时,求点E运动的时间t的值,并直接写出点G从出发到此时所经过的路径长 (即线段AG的长).
时,求点E运动的时间t的值,并直接写出点G从出发到此时所经过的路径长 (即线段AG的长).
【答案】(1)![]() t,4﹣
t,4﹣![]() t;(2)t=2或2
t;(2)t=2或2![]() ﹣2(3)
﹣2(3)![]()
【解析】分析:(1)依据△CDO和△CEF均为等腰直角三角形,CE=![]() t,即可得到点G的坐标;
t,即可得到点G的坐标;
(2)依据∠OCE=∠BFG=45°,分两种情况进行讨论:①若△OCE∽△BFG,则![]() ,②若△ECO∽△BFG,则
,②若△ECO∽△BFG,则![]() ,分别求得t的值即可;
,分别求得t的值即可;
(3)过点G作GH∥x轴,交AB于H,根据直线AB的解析式为y=-2x+12,根据G(![]() t,4-
t,4-![]() t),将y=4-
t),将y=4-![]() t代入y=-2x+12,可得H(4+
t代入y=-2x+12,可得H(4+![]() ,4-
,4-![]() t),再根据△ABG 的面积为
t),再根据△ABG 的面积为![]() ,即可得到t的值,进而得到点G的坐标为(
,即可得到t的值,进而得到点G的坐标为(![]() ,
,![]() ),CG=
),CG=![]() .
.
详解:(1)由题可得,△CDO和△CEF均为等腰直角三角形,
∵CE=![]() t,
t,
∴CF=EF=t,
∴点G的横坐标为CF+![]() EF=t+
EF=t+![]() t=
t=![]() t,纵坐标为CO-
t,纵坐标为CO-![]() EF=4-
EF=4-![]() t,
t,
∴G(![]() t,4-
t,4-![]() t),
t),
故答案为:![]() t,4-
t,4-![]() t;
t;
(2)∵CE=![]() t,
t,
∴EF=CF=t,FG=![]() t,BF=4-t,
t,BF=4-t,
∵∠OCE=∠BFG=45°,
①若△OCE∽△BFG,则![]() ,
,
即![]() ,解得t=2;
,解得t=2;
②若△ECO∽△BFG,则![]() ,
,
即![]() ,解得t=2
,解得t=2![]() -2;
-2;
综上所述,当t=2或2![]() -2时,以O、C、E为顶点的三角形与△BFG相似;
-2时,以O、C、E为顶点的三角形与△BFG相似;
(3)如图,过点G作GH∥x轴,交AB于H,
设直线AB的解析式为y=kx+b,则
![]() ,解得
,解得![]() ,
,
∴y=-2x+12,
∵G(![]() t,4-
t,4-![]() t),将y=4-
t),将y=4-![]() t代入y=-2x+12,可得x=4+
t代入y=-2x+12,可得x=4+![]() ,
,
∴H(4+![]() ,4-
,4-![]() t),
t),
∴GH=|4+![]() -
-![]() t|,
t|,
∴S△ABG=![]() GH×BD=
GH×BD=![]() |4+
|4+![]() -
-![]() t|×4=2|4-
t|×4=2|4-![]() t|,
t|,
又∵△ABG 的面积为![]() ,
,
∴2|4-![]() t|=
t|=![]() ,
,
解得t=![]() 或t=
或t=![]() (舍去),
(舍去),
此时,点G的坐标为(![]() ,
,![]() ),CG=
),CG=![]() .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.