题目内容
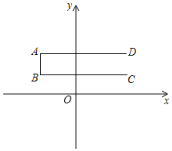
【题目】如图,在矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是![]() ,将
,将![]() 沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.

(1)求直线OB的解析式及线段OE的长.
(2)求直线BD的解析式及点E的坐标.
【答案】(1)直线OB的解析式为![]() ,
,![]() ;(2)直线BD的解析式为
;(2)直线BD的解析式为![]() ,
,![]() .
.
【解析】
(1)先利用待定系数法求直线OB的解析式,再利用两点间的距离公式计算出OB,然后根据折叠的性质得到BE=BC=6,从而可计算出OE=OB-BE=4;
(2)设D(0,t),则OD=t,CD=8-t,根据折叠的性质得到DE=DC=8-t,∠DEB=∠DCB=90°,根据勾股定理得(8-t)2+42=t2,求出t得到D(0,5),于是可利用待定系数法求出直线BD的解析式;设E(x,![]() ),利用OE=4得到x2+(
),利用OE=4得到x2+(![]() )2=42,然后解方程求出x即可得到E点坐标.
)2=42,然后解方程求出x即可得到E点坐标.
解:(1)设直线OB的解析式为![]() ,
,
将点![]() 代入
代入![]() 中,得
中,得![]() ,
,
∴![]() ,
,
∴直线OB的解析式为![]() .
.
∵四边形OABC是矩形.且![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
根据勾股定理得![]() ,
,
由折叠知,![]() .
.
∴![]()
(2)设D(0,t)
![]() ,
,
∴![]() ,
,
由折叠知,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
根据勾股定理得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
设直线BD的解析式为![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线BD的解析式为![]() .
.
由(1)知,直线OB的解析式为![]() .
.
设点![]() ,
,
根据![]() 的面积得
的面积得![]() ,
,
∴![]() ,
,
∴![]() .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】我们在生活中经常使用的数是十进制数,如![]() ,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字
,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字![]() 和字母
和字母![]() 共16个计数符号,这些符号与十进制的对应关系如下表
共16个计数符号,这些符号与十进制的对应关系如下表
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如:十六进制数![]() ,即十六进制数71B相当于十进制数1819.那么十六进制数2E8相当于十进制数( )
,即十六进制数71B相当于十进制数1819.那么十六进制数2E8相当于十进制数( )
A.744B.736C.536D.512